Straight Line
Straight Line Important Formulae
- Find and interpret equation of a straight line in various forms.
- Perform slope calculations including parallel and perpendicular lines.
- Find angle between two coplanar, non-parallel lines.
- Calculate distance between two points in space.
Slope of a Straight Line
Slope of a straight line gives you an idea about its inclination with reference to x-axis. Slope is also referred as gradient.
\[\mathrm{Slope \ of \ a \ straight \ line} = \dfrac{\mathrm{Rise}}{\mathrm{Run}} = \dfrac{\Delta y}{\Delta x}\]Equation of a Straight Line
The equation of a straight line (or any curve) is the relation between the x and y (and z) coordinates of all points lying on it.
The general form of the equation of a straight line is:
Various forms of equations of Straight Line
Slope Point Format:
where \(x_{1}\) and \(y_{1}\) are the coordinates of the point through which the line passes.
Slope Intercept Format:
where m = slope and b = y-intercept
For the above line, y-intercept = 1, and
slope = \(\dfrac{\mathrm{Rise}}{\mathrm{Run}}\) = \(\dfrac{2}{4}\) = \(\dfrac{1}{2}\)
So the equation will be, \[y = 0.5x + 1\] \[2y = x + 2\] \[x - 2y + 2 = 0\]
Double Intercept Format:
\[\dfrac{x}{a}+\dfrac{y}{b} = 1\]
where a = x intercept and b = y intercept
Parallel and Perpendicular Lines
For parallel lines slopes are equal i.e. \(m_{1} = m_{2}\)
For perpendicular lines
\[m_{1} * m_{2} = -1\]
or,
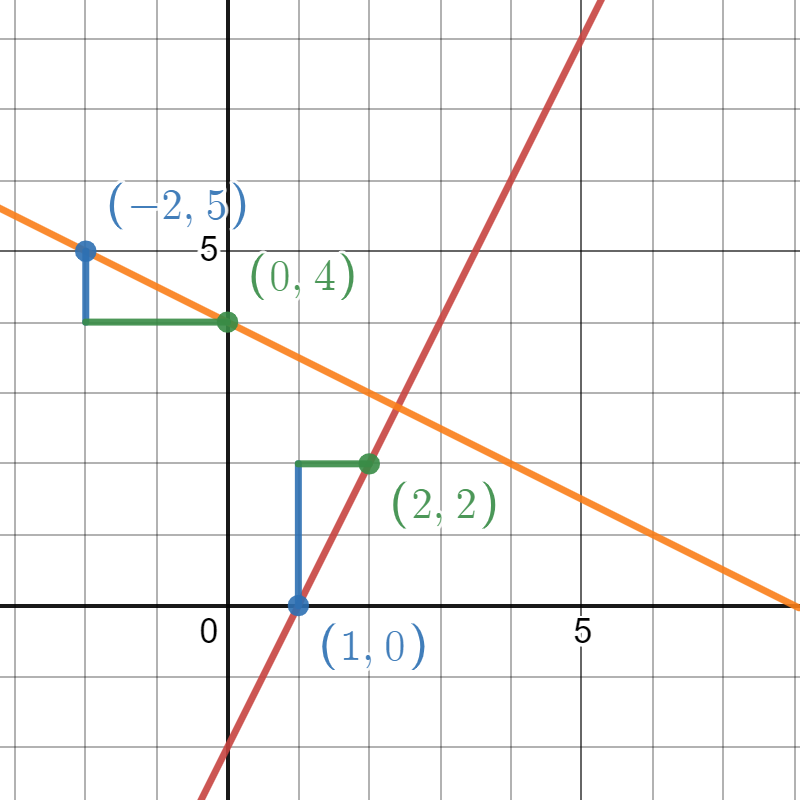
Brigban, CC0, via Wikimedia Commons
Angle between Two Lines
Angle between two straight lines is given by:
Distance Formula
Distance between two points in the space \(P_1\) \((x_1,y_1,z_1)\) and \(P_2\) \((x_2,y_2,z_2)\) is given by:
This can be proved by repeated application of the Pythagorean Theorem.
Jim.belk, Public domain, via Wikimedia Commons
Fill in the Blank Questions:
True/False Questions:
Matching Questions:
Match the following terms to their definitions:
- Slope
- Y-intercept
- Standard form
- Perpendicular lines
- Parallel lines
- The point where the line crosses the y-axis
- Lines that intersect at right angles
- The ratio of vertical change to horizontal change
- Lines that never intersect
- The form Ax + By = C