Learning Objectives:

• Determine the change in an object’s kinetic energy and speed that results from the application of specified forces.

Kinetic Energy of an object is the energy that it possesses due to its motion. The kinetic energy of a non-rotating object of mass m traveling at a speed v is:

$T = \dfrac{1}{2} mv^2$       Page 107

KoenB, Public domain, via Wikimedia Commons

Solved Example: 23423

When an object rolls down a hill, its potential energy is converted to:

A. Thermal energy.

B. Chemical energy.

C. Kinetic energy.

D. Sound energy.

Correct Answer: C

Solved Example: 31-1-01

A body possesses linear momentum 2 kg.m/s and kinetic energy of 2J. The mass of the body is:

A. 0.5 kg

B. 1.42 kg

C. 1 kg

D. 2 kg

Linear momentum, \[mv = 2\] Also, kinetic energy, \[\dfrac{1}{2} mv^2 = 2\] Dividing these two equations, we get \[\dfrac{2}{v} = 1\] \[v = 2\ \mathrm{m/s}\] Substituting in the first equation, m = 1 kg

Correct Answer: C

Solved Example: 31-1-02

The kinetic energy of a particle having mass m is E. Its momentum will be:

A. 2 mE

B. $\sqrt{\dfrac{1}{2} mE}$

C. $\sqrt{2 mE}$

D. $\dfrac{1}{2} mE$

\[KE = \dfrac{1}{2}mv^2\] Given KE = E, \begin{align*} E &= \dfrac{1}{2}mv^2\\ 2E &= mv^2\\ \dfrac{2E}{m} &= v^2\\ \sqrt{\dfrac{2E}{m}} &= v\\ \end{align*} Momentum is given by, \begin{align*} M &= mv\\ &= m \times \sqrt{\dfrac{2E}{m}}\\ &= \sqrt{m} \sqrt{m} \times \sqrt{\dfrac{2E}{m}}\\ &= \sqrt{m} \times \sqrt{2E}\\ &= \sqrt{2mE}\\ \end{align*}

Correct Answer: C

Solved Example: 31-1-03

During an object's free fall, which of the following energies increases at one point in its path?

A. Kinetic energy

B. Chemical energy

C. Potential energy

D. Mechanical energy

During an object's free fall, potential energy keeps on decreasing as the elevation gets reduced, but at the same time, since the velocity of the object is increasing, its kinetic energy increases continuously.

Correct Answer: A

Solved Example: 31-1-04

What type of energy conversion takes place during the thunder of clouds?

A. Frictional energy is converted into light and sound energy.

B. Kinetic energy is converted into light and sound energy.

C. Potential energy is converted into light and sound energy.

D. Kinetic energy is converted into electrostatic energy.

When clouds collide, their kinetic energy is converted into light and sound.

Correct Answer: B

Solved Example: 31-1-05

A Fan consumes 200 W of electric power and discharges air from a ventilation room at the rate of 1 kg/s. What will be the positive air velocity from the fan?

A. 200 m/s

B. 20 m/s

C. 42 m/s

D. 4.2 m/s

\begin{align*} \Delta E &= \dfrac{1}{2} mv^2\\ (\dot{\Delta E}) &= \dfrac{1}{2} \dot{m}v^2\\ \mathrm{Power} &= \dfrac{1}{2} \dot{m}v^2\\ 200 &= \dfrac{1}{2} (1)v^2\\ 400 &= v^2\\ v &= 20\ \mathrm{m/s} \end{align*}

Correct Answer: B

Learning Objectives:

• Calculate the gravitational potential energy of a particle in various situations.
• Calculate the elastic potential energy of a particle attached to a stretched spring.

Solved Example: 31-2-01

Jack climbs a mountain via a short, steep trail. Jill ascends the same mountain via a long and considerably less steep path. Which of the following statements is true? Assume that Jack and Jill have the same mass.

A. Jack gains more gravitational potential energy than Jill.

B. Jack gains less gravitational potential energy than Jill.

C. Jack gains the same gravitational potential energy as Jill.

D. To compare gravitational potential energies, we must know the height of the mountain.

$\Delta U = mgh$, same h for both. So gravitational potential energy is same.

Reference: http://resources.seattlecentral.edu

Correct Answer: C

Solved Example: 31-2-02

A compressed spring possesses _________.

A. Electric energy

B. Chemical energy

C. Potential energy

D. Kinetic energy

Correct Answer: C

Solved Example: 31-2-03

A ball is dropped from a height h and rebounds to a height which is 80% of the initial height. Find the ratio of final potential energy to the initial potential energy of the ball.

A. $\dfrac{5}{4}$

B. $\dfrac{4}{5}$

C. $\dfrac{25}{4}$

D. $\dfrac{4}{25}$

Original Potential Energy = mgh
Final Potential Energy = 0.8 mgh

Ratio = 0.8 = $\dfrac{4}{5}$

Correct Answer: B

Solved Example: 31-2-04

The energy possessed by a body by virtue of its position is called the _________.

A. Electrostatic Energy

B. Kinetic Energy

C. Conservative Energy

D. Potential Energy

• Potential Energy is the energy possessed by a body by virtue of its position. \[PE = mgh\]
• Kinetic Energy is the energy possessed by a body by virtue of its velocity. \[KE = \dfrac{1}{2}mv^2\]

Correct Answer: D

Solved Example: 31-2-05

A particle of mass 1 kg is attached to one end of a spring having stiffness of 1250 N/m. The free length of the spring is 1000 mm. The system is rotated about the other end of the spring at a uniform angular velocity of 5 rad/s. Ignore gravity and consider that the elongation of the spring may be considered negligible to the free length of the spring. The elongation of the spring (in mm) is:

A. 10 mm

B. 20 mm

C. 25 mm

D. 27.5 mm

Centrifugal acceleration is given by, \begin{align*} F &= m r \omega^2\\ F &= (1) (1) (5)^2\\ F &= 25\ \mathrm{N} \end{align*} \begin{align*} \delta &= \dfrac{F}{k}\\ &= \dfrac{25}{1250}\\ &= \dfrac{25}{1250}\\ &= 0.02\ m = 20\ \mathrm{mm} \end{align*}

Correct Answer: B

Learning Objectives:

• Calculate the work done by a specified constant force on an object that undergoes a specified displacement.
• Relate the work done by a force to the area under a graph of force as a function of position, and calculate this work in the case where the force is a linear function of position.

Solved Example: 23423

The work done on an object is equal to:

A. The energy the object has.

B. The force applied multiplied by the distance moved in the direction of the force.

C. The mass of the object.

D. The speed of the object.

Correct Answer: B

Solved Example: 31-1-04

Which of the following is a conservative force?

A. Frictional force

B. Spring force

C. Drag force

D. Magnetic force

Correct Answer: B

Solved Example: 31-1-05

If the work done by a non-zero force is zero, it means:

A. The displacement must be zero.

B. The force must be perpendicular with the displacement.

C. Either (A) or (B)

D. None of the above.

Correct Answer: C

Solved Example: 31-3-01

A truck driver slams on the brakes of a moving truck with a constant velocity v, as a result of his action the truck stops after traveling a distance d. If the driver had been traveling with twice the velocity, what would be the stopping distance compared to the distance in the first trial?

A. Two times greater

B. Four times greater

C. The same

D. Half as much

The acceleration (in this case retardation) depends upon Force and mass, both of which are unchanged in two cases. Hence $a= \dfrac{F}{m}$ will remain unchanged irrespective of the velocity.

Here the final velocity(v) is zero, initial velocity (u) is $V_{initial}$
Using, \begin{align*} v^2 &= u^2 + 2as\\ 0 &= u^2 + 2as\\ u^2 &= -2as\\ s &= -\dfrac{u^2}{2a} \end{align*} Hence, the stopping distance is proportional to the square of initial velocity, provided other parameters remain same. That means, if truck speed is doubled, the stopping distance will now be four times greater.

Correct Answer: B

Solved Example: 31-3-02

The work done by a person in carrying a box of mass 15 kg through a vertical height of 5 m is 5000 J. The mass of the person is _______ Take g = 10 m/s$^2$.

A. 95 kg

B. 45 kg

C. 65 kg

D. 85 kg

Let 'x' be the mass of the person. Hence, the combined mass (person + box) raised will be (x+ 15)kg. \begin{align*} W &= mgh\\ 5000 &= (x + 15) \times 10 \times 5\\ x + 15 &= 100\\ x &= 85\ \mathrm{kg} \end{align*}

Correct Answer: D

Solved Example: 31-3-03

If a box of mass 25 kg is pushed 15 m by a force of 'F' N and work done in the process is 480 J. Find F:

A. 50 N

B. 32 N

C. 16 N

D. 25 N

\begin{align*} W &= F. s\\ 480 &= F. 15\\ F &= 32\ \mathrm{N} \end{align*}

Correct Answer: B

Solved Example: 31-3-04

A particle moves from a point $-2\bar{i} + 5\bar{j}$ to $4\bar{j} + 3\bar{k}$ when a force of $4\bar{i}- 3\bar{j}$ N is applied. How much work has been done by the force?

A. 8 J

B. 11 J

C. 5 J

D. 2 J

The displacement is given by: \begin{align*} s &= (4\bar{j} + 3\bar{k}) - (-2\bar{i} + 5\bar{j})\\ &= (2\bar{i} - \bar{j} + 3\bar{k}) \end{align*} Work done is given by, \begin{align*} W &= \bar{F} \cdot \bar{s}\\ &= (4\bar{i}- 3\bar{j}) \cdot (2\bar{i} - \bar{j} + 3\bar{k})\\ &= ((4)(2) + (-3)(-1)) + (0)(3))\\ &= (8 + 3 + 0)\\ &= 11\ \mathrm{J} \end{align*}

Correct Answer: B

Solved Example: 31-3-05

A force increases the speed of a 1.0 kg object from 4 m/s to 8 m/s. The work done by the force will be:

A. 8 J

B. 32 J

C. 24 J

D. 16 J

Work done = Increase in Kinetic Energy \begin{align*} W &= \dfrac{1}{2} mv^2 - \dfrac{1}{2} mu^2\\ &= \dfrac{1}{2} (1)(8)^2 - \dfrac{1}{2} (1)(4)^2\\ &= 32 - 8\\ &= 24\ \mathrm{J}\\ \end{align*}

Correct Answer: C

Learning Objectives:

• Determine the mechanical power generated by an engine or electrical power generated by a motor.
• Calculate the mechanical efficiency correlating electrical and mechanical power in case of motor and shaft combination.

Mechanical Power is the rate of doing work. It is equivalent to an amount of energy consumed per unit time. In the MKS system, the unit of power is the joule per second (J/s), known as the Watt in honor of James Watt. Larger units are 1KW = 1000 W or 1 Horsepower (HP) = 746 W.
Mechanical Power,

Solved Example: 31-4-01

Amount of energy supplied by current in unit time is called:

A. Electric energy

B. Friction

C. Resistance

D. Electric power

Power is rate of work done (or energy supplied). \[\mathrm{Power} = \dfrac{\mathrm{Energy}}{\mathrm{time}}\] \[P = \dfrac{E}{t}\]

Correct Answer: D

Solved Example: 31-4-02

A 220 $\Omega$ resistor dissipates 3 W. The voltage is:

A. 73.3 V

B. 2.5 V

C. 25.7 V

D. 257 V

Using, \[P = VI = I^2R = \dfrac{V^2}{R}\] Substituting the values, \begin{align*} P &= \dfrac{V^2}{R}\\ 3 &= \dfrac{V^2}{220}\\ V^2 &= 220 \times 3\\ V &= 25.7\ V \end{align*}

Correct Answer: C

Solved Example: 31-4-03

A particle of mass 0.2 kg is moving in one dimension under a force that delivers a constant power 0.5 W to the particle. If the initial speed (in m/s) of the particle is zero, the speed (in m/s) after 5 s is:

A. 2.0

B. 2.5

C. 5.0

D. 5.6

Power is rate of Energy. \begin{align*} P &=\dfrac {dE}{dt}\\ P &=\dfrac {d}{dt}\left( \dfrac {1}{2}mv^{2}\right) \\ P &=\dfrac {1}{2}m\dfrac {d}{dt}\left( v^{2}\right) \\ \dfrac {2P}{m}&=2v\dfrac {dv}{dt}\\ \dfrac {P}{m}dt&=vdv\\ \int ^{t}_{0}\dfrac {P}{m}dt&=\int ^{v}_{0}vdv\\ \dfrac {P}{m}t&=\dfrac {v^{2}}{2}\\ v^{2}&=\dfrac {2\times 0.5\times 5}{0.2}\\ v^{2}&=25\\ v&=5\ \mathrm{m/s} \end{align*}

Correct Answer: C

Solved Example: 31-4-04

Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of the input energy. How much power is generated by the turbine? (g=10 m/s$^2$)

A. 10.2 kW

B. 8.1 kW

C. 12.3 kW

D. 7.0 kW

\begin{align*} v &= \sqrt{2 g H}\\ &= \sqrt{2 (10) (60)}\\ &= 34.64\ \mathrm{m/s} \end{align*} \begin{align*} P = (\dot{KE}) &= \dfrac{1}{2}\dot{m} v^2\\ &= \dfrac{1}{2}(15) (1200)\\ &= 9000\ \mathrm{W} \end{align*} However, 10% energy is lost due to frictional forces. \[P = 0.9 \times 9000 = 8100\ \mathrm{W} =8.1\ \mathrm{kW}\]

Correct Answer: B

Solved Example: 31-4-05

The power required to lift a mass of 8 kg up a vertical distance of 4 m in 2 s is (taking acceleration due to gravity as 10 m/s$^2$

A. 80 W

B. 160 W

C. 320 W

D. 640 W

\begin{align*} P &= \dfrac{W}{t}\\ &= \dfrac{mgh}{t}\\ &= \dfrac{(8)(10)(4)}{2}\\ &= 160\ \mathrm{W} \end{align*}

Correct Answer: B

Solved Example: 31-4-06

The power of a water pump is 2 kW. The amount of water (in litres) it can raise in one minute to a height of 10 m will be:

A. 100

B. 1000

C. 1200

D. 2000

\begin{align*} P &= \dfrac{W}{t}\\ &= \dfrac{mgh}{t}\\ 2 \times 10^3 &= \dfrac{m(10)(10)}{60}\\ \dfrac{2 \times 10^3 \times 60}{100} &= m\\ m &= 1200\ \mathrm{kg} \end{align*} \begin{align*} \rho &= \dfrac{m}{V}\\ V &= \dfrac{m}{\rho}\\ &= \dfrac{1200}{1000}\\ &= 1.2\ m^3 = 1200\ \mathrm{liters} \end{align*}

Correct Answer: C

Learning Objectives:

• Interpret (and provide) examples that illustrate the law of conservation of energy such as transformation from potential and kinetic energy, and vice versa.

If T\(_i\) and V\(_i\) are, respectively, the kinetic and potential energy of a particle at state i, then for conservative systems (no energy dissipation or gain), the law of conservation of energy is:

$T_2 + V_2 = T_1 + V_1$       Page 106

If nonconservative forces are present, then the work done by these forces must be accounted for. Hence

$T_2 + V_2 = T_1 + V_1 + U_{1 \rightarrow 2}$       Page 106

where \(U_{1 \rightarrow 2}\) = the work done by the nonconservative forces in moving between state 1 and state 2.
Care must be exercised during computations to correctly compute the algebraic sign of the work term.

• If the forces serve to increase the energy of the system, U\(_{1 \rightarrow 2}\) is positive.
• If the forces, such as friction, serve to dissipate energy, U\(_{1 \rightarrow 2}\) is negative.

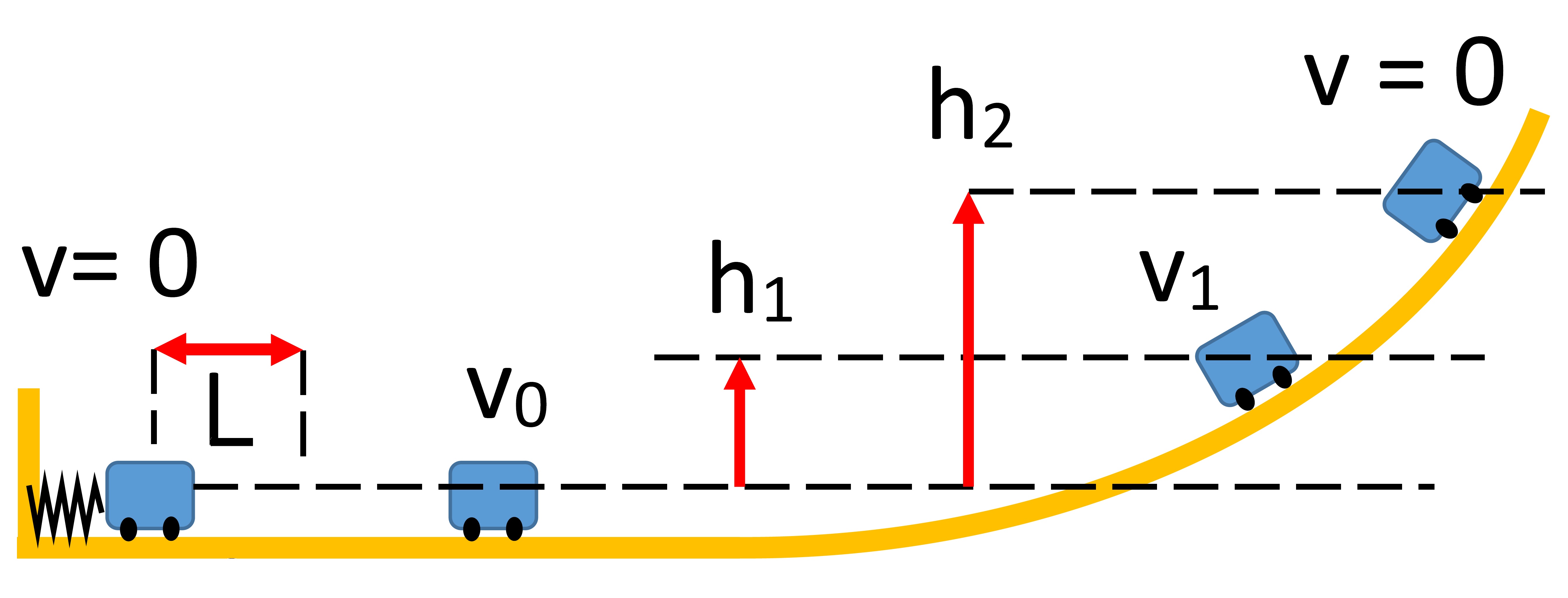
Guy vandegrift, CC BY-SA 3.0, via Wikimedia Commons

Solved Example: 31-5-01

Energy can neither be created nor be destroyed, but it can be changed from one form to another", this law is known as:

A. Kinetic energy

B. Potential energy

C. Conservation of energy

D. Conservation principle

Correct Answer: C

Solved Example: 31-5-02

What cannot happen to energy according to the law of conservation of energy?

A. Energy cannot be transformed.

B. Energy cannot be created

C. Energy cannot be changed.

D. Energy cannot be converted.

According to the law of conservation of energy:

• Energy cannot be created.
• Energy cannot be destroyed.
• However, energy can be converted from one form to another.

Correct Answer: B

Solved Example: 31-5-03

Energy cannot be created nor destroyed, only changed from one form to another. How does listening to music on a radio obey the law of conservation of energy?

A. Sound energy is changed into potential energy.

B. Electrical energy is gradually destroyed as the radio plays.

C. Electrical energy remains unchanged.

D. Electrical energy is converted into other forms of energy, such as sound.

Correct Answer: D

Solved Example: 31-5-04

A 5 kg block slides down a frictionless incline that is 10 meters high. If the block starts from rest at the top of the incline, what is its speed at the bottom of the incline?

A. $10 \, \text{m/s}$

B. $14 \, \text{m/s}$

C. $20 \, \text{m/s}$

D. $28 \, \text{m/s}$

\[PE_{\text{initial}} = mgh = 5 \, \text{kg} \times 9.8 \, \text{m/s}^2 \times 10 \, \text{m} = 490 \, \text{J}\] \[PE_{\text{initial}} = KE_{\text{final}}\] \[490 \, \text{J} = \dfrac{1}{2} m v^2\] \[490 = \dfrac{1}{2} \times 5 \times v^2\] \[490 = 2.5 \times v^2\] \[v^2 = \dfrac{490}{2.5} = 196\] \[ v = \sqrt{196} = 14 \, \text{m/s} \]

Correct Answer: B

Solved Example: 5645656

When a spring is compressed, it stores:

A. Kinetic energy

B. Potential energy

C. Thermal energy

D. Chemical energy

Correct Answer: B