Processes
Thermodynamic Processes
Learning Objectives:
- Define a thermodynamic process.
- Understand the difference between reversible and irreversible process.
- State characteristics of common processes observed in thermodynamics and derive work done and heat transfer equations.
- Generalize these common processes with the help of a single polytropic process.
- Explain the differences among the simple thermodynamic processes-isobaric, isochoric, isothermal, and adiabatic.
A process occurs when the system undergoes a change in state due to energy transfer at a steady state. A process may be non-flow in which a fixed mass within the defined boundary is undergoing a change of state.
Example: A substance which being heated in a closed cylinder undergoes a non-flow process or closed system undergoes non-flow process.
A process may be a flow process in which mass is entering and leaving through boundary of an open system. In a steady flow process mass is crossing the boundary from surroundings at entry and an equal mass is crossing the boundary at the exit so that the total mass of the system remains constant.
Quasi-static process:
Quasi means almost. A quasi- static process is also called as reversible process. This process is a succession of equilibrium states and infinite slowness is its characteristic feature.
Reversible process:
A reversible process (also sometimes known as quasi-static process) is one which can be stopped at any stage and reversed so that the system and surroundings are exactly restored to their initial states. This process has the following characteristics:
- It must pass through the same states on the reversed path as were initially visited on the forward path.
- This process when undone will leave no history of events in the surroundings.
- It must pass through a continuous series of equilibrium states.
Examples: Some examples of nearly reversible processes are: Frictionless relative motion, Expansion and compression of spring, Frictionless adiabatic expansion or compression of fluid, Isothermal expansion or compression, Electrolysis.
Irreversible process:
An irreversible process is one in which heat is transferred through a finite temperature difference and usually represented by a dotted (or discontinuous) line joining the end states.
Examples: Relative motion with friction, Combustion, Free expansion, Diffusion, Electricity flow through resistance, Plastic deformation, Heat transfer. Irreversibilities are of two types:
-
External Irreversibilities: These are associated with dissipating effect outside the working fluid. Example: Mechanical friction occurring during a process due to some external source.
-
Internal Irreversibilities: These are associated with dissipating effects within the working fluid. Example: Unrestricted expansion of gas, viscosity and inertia of the gas.
Solved Example: 72-1-01
In an open system, for maximum work, the process must be entirely
A. Irreversible
B. Reversible
C. Adiabatic
D. None of the mentioned
A reversible process gives the maximum work.
Correct Answer: B
Solved Example: 72-1-02
Which of the following is true for a closed system?
A. Mass entering = mass leaving
B. Mass does not enter or leave the system
C. Mass entering can be more or less than the mass leaving
D. None of the mentioned
For a closed system mass does not change.
Correct Answer: B
Isochoric Process- Constant Volume
Learning Objectives:
- Calculate total work done in a Constant Volume thermodynamic process.
A constant volume process is the vertical path dV = 0 in the P-V plane - up if heat is added and down if heat is removed. Because dV = 0, the work done is
The First Law of Thermodynamics then states: \[dU= dQ + dW = dQ + 0 = dQ\] \[dQ = dU = mC_V(T_2 - T_1)\]
Solved Example: 72-2-01
Isochoric process is one in which:
A. Free expansion takes place
B. Very little mechanical work is done by the system
C. No mechanical work is done by the system
D. All parameters remain constant
In isochoric process, volume remains constant. Hence, there is no mechanical work done by the system.
Correct Answer: C
Solved Example: 72-2-02
If a gas is heated against a pressure, keeping the volume constant, then work done will be equal to:
A. Positive
B. Negative
C. Zero
D. Pressure $\times$ volume
As long as the volume remains constant, there is no work done.
Correct Answer: C
Solved Example: 72-2-03
If 2 bar of air at 27$^\circ$C is heated to 177$^\circ$C at constant volume, the pressure will be:
A. 6.56 bar
B. 3 bar
C. 9 bar
D. 13.11 bar
Correct Answer: B
Isobaric Process- Constant Pressure
Learning Objectives:
- Calculate total work done in a constant pressure thermodynamic process.
A process in which pressure remains constant.
A constant pressure process is a horizontal path in the P-V diagram - right for expansion and left for compression. Example: a gas in a container sealed with a freely-sliding massive piston.
The work done during gas expansion is: \[dw = - P dv\]
\[w = \int_1^2 P dv = P \int_1^2 dv = P(v_2 - v_1)\]
\[Q = \int_1^2 mC_P dT = m C_P (T_2 - T_1)\]
By Applying first law of thermodynamics, \[Q - W = \Delta U\] \[m C_P (T_2 - T_1) - mR (T_2 - T_1) = m C_V (T_2 - T_1)\]
This is also known as Meyer’s formula.
Solved Example: 72-3-01
Addition of heat at constant pressure to a gas results in:
A. Raising its temperature
B. Raising its pressure
C. Raising its volume
D. Raising its temperature and doing external work
Correct Answer: D
Solved Example: 72-3-02
A piston/cylinder device contains one kilogram of a substance at 0.8 MPa with a specific volume of 0.2608 m$^3$ /kg. The substance undergoes an isobaric process until its specific volume becomes 0.001115 m$^3$/kg. Find the total work done in the process.
A. 147.7 kJ
B. 207.7 kJ
C. 215.5 kJ
D. 274.1 kJ
\begin{align*} P_{1} &=0.8\times 10^{6} Pa\\ V_{1} &=0.2608 \dfrac {m^{3}}{kg}\\ V_{2} &=0.001115 \dfrac {m}{kg} \end{align*} \begin{align*} W &= PdV \\ &=0.8\times 10^{6}\times \left[ 0.001115-0.2608\right] \\ &=207.7\ kJ \end{align*}
Correct Answer: B
Solved Example: 72-3-03
When an ideal diatomic gas is heated at constant pressure, the fraction of the heat energy supplied which increases the internal energy of the gas, is:
A. $\dfrac{2}{5}$
B. $\dfrac{3}{5}$
C. $\dfrac{3}{7}$
D. $\dfrac{5}{7}$
\[ f = \dfrac{\Delta U}{\Delta Q} = \dfrac{m C_v \Delta T}{m C_p \Delta T} = \dfrac{C_v}{C_p} = \dfrac{1}{\gamma}\] For ideal diatomic gas, $\gamma$ = $\dfrac{7}{5}$ \[f = \dfrac{5}{7}\]
Correct Answer: D
Isothermal Process- Constant Temperature
Learning Objectives:
- Calculate total work done in a Constant Temperature thermodynamic process.
A process in which the temperature of the system is constant.
A constant temperature process is an isothermal path in the P-V diagram—a hyperbolic isotherm. Example: a gas in a container that is immersed in a constant-temperature bath is allowed to expand slowly, or is compressed slowly.
At constant temperature, the pressure of an ideal gas is: \[PV = C\] \[P = \dfrac{C}{V}\]
The work done on the gas is: \[W = \int_{V_1}^{V_2} P\ dV\] \[W = \int_{V_1}^{V_2} \dfrac{C}{V}\ dV\] \[W = p_1 V_1 \ln\left(\dfrac{V_2}{V_1}\right)\] The First Law gives: \[dU = dQ - dW = 0\] \[dQ = dW\]
In an isothermal process, there is no change in the internal energy of an ideal gas.
Netheril96, CC0, via Wikimedia Commons
Solved Example: 72-4-01
An isothermal process is governed by:
A. Boyle's law
B. Charles' law
C. Gay-Lussac law
D. Avogadro's law
An isothermal process is governed by Boyle's law, whereas isobaric process is governed by isobaric process is governed by Charle's law.
Correct Answer: A
Solved Example: 72-4-02
In an isothermal process:
A. q = 0, $\Delta$U = 0
B. q $\neq$ 0, $\Delta$U = 0
C. q = 0, $\Delta$U $\neq$ 0
D. q $\neq$ 0, $\Delta$U $\neq$ 0
In an isothermal process, $\Delta T$ = 0. Since the internal energy is the function of temperature, $\Delta U$ is also = 0. But in an isothermal process, heat can be added or rejected, hence $\Delta Q$ is not zero.
Correct Answer: B
Solved Example: 72-4-03
A cylinder contains 5 m$^3$ of an ideal gas at a pressure of 1 bar. This gas is compressed in a reversible isothermal process till its pressure increases to 5 bar. The work in kJ required for this process is:
A. 981.7
B. 1012.2
C. 953.2
D. 804.7
$V_1 = 5\ m^3, P_1 = 1\ \mathrm{bar}, P_2 = 5\ \mathrm{bar}$
Work done in isothermal process,
\begin{align*}
&= mRT_1 \log \dfrac{P_1}{P_2}\\
&= P_1 v_1 \log \dfrac{P_1}{P_2}\\
&= 1 \times 10^5 \times 5 \log \left(\dfrac{1}{5}\right)\\
&= 804.718\ \mathrm{KJ}
\end{align*}
Correct Answer: D
Solved Example: 72-4-04
Air with mass of 1 kg and initially at P = 101.3 kPa is contained within a cylinder and has a specific volume of 0.850 m$^3$ /kg. The piston within the cylinder has a diameter of 0.2 m. A cup on top of the piston is then filled at a constant rate until it contains 50 kg of water, thus compressing the air. The compression proceeds slowly and the air undergoes a process where Pv = constant. Calculate the work done on the gas during the process.
A. 12.4 kJ
B. 15.4 kJ
C. 18.2 kJ
D. 22.1 kJ
\[P_2 = 101.3 kPa + \dfrac{50 \times 9.81}{\dfrac{\pi}{4}(0.2)^2} = 116.9\ kPa\] Using P$_2$v$_2$ = constant, \[v_2 = 0.736\ m^3/kg\] \[W_{out} = m . \mathrm{constant}. \ln \left(\dfrac{v_2}{v_1}\right) \quad W_{out} = 1 \times 86.105 \times \ln \left(\dfrac{0.736}{0.850}\right) \quad W_{out} = -12.4 kJ\] \[W_{in} = - W_{out} = 12.4 kJ\]
Correct Answer: A
Solved Example: 72-4-05
Air enters a compressor at 1 bar and 25$^\circ$C having volume of 1.8 m$^3$/kg and is compressed to 5 $\times$ 10$^5$ isothermally. Determine Heat transferred.:
A. -125.80 KJ
B. -157.53 KJ
C. -289.70 KJ
D. -331.31 KJ
\[ v_2 = \dfrac{P_1 v_1}{P_2} = \dfrac{10^5 \times 1.8}{5 \times 10^5} = 0.36 m^3/kg\] \[W = -125.8 kJ/kg\] Change in internal energy, \[dU = U_2 -U_1 =0\] \[ \Delta Q = \Delta W = -125.8 kJ/kg\]
Correct Answer: A
Adiabatic Process
Learning Objectives:
- Calculate total work done in an adiabatic process.
A process in which the system is enclosed by adiabatic wall.
In an adiabatic process no heat is added to or removed from the gas (i.e., Q= 0). Examples include systems insulated so no heat is exchanged with the surroundings, and systems in which processes happen so fast that there is no time to add or remove heat. Because Q = 0 for an adiabatic process the First Law of Thermodynamics tells us that \(\Delta E = -W\). The energy for any work done comes from the change in the system’s internal energy.
where \(k = \dfrac{C_p}{C_v}\) is the ratio of the heat capacity at constant pressure to the heat capacity at constant volume.
MikeRun, CC BY-SA 4.0, via Wikimedia Commons
Solved Example: 72-5-01
A process, in which the working substance neither receives nor gives out heat to its surroundings during its expansion or compression, is called:
A. Isothermal process
B. Hyperbolic process
C. Adiabatic process
D. Polytropic process
Correct Answer: C
Solved Example: 72-5-02
Adiabatic process is:
A. Essentially an isentropic process
B. Non-heat transfer process
C. Reversible process
D. Constant temperature process
Correct Answer: B
Solved Example: 72-5-03
Work done in an adiabatic process between a given pair of end states depends on:
A. The end states only
B. Particular adiabatic process
C. The value of index n
D. The value of heat transferred
Correct Answer: A
Solved Example: 72-5-04
An isolated system is one in which:
A. Mass does not cross boundaries of the system, though energy may do so
B. Neither mass nor energy crosses the boundaries of the system
C. Both energy and mass cross the boundaries of the system
D. Mass crosses the boundary but not the energy
Correct Answer: B
Solved Example: 72-5-06
The ratio of specific heat at constant pressure (C$_p$) and specific heat at constant volume (C$_v$) is:
A. Equal to one
B. Less than one
C. Greater than one
D. None of these.
Correct Answer: C
Solved Example: 72-5-07
Characteristic gas constant of a gas is equal to:
A. $\dfrac{C_p}{C_v}$
B. $\dfrac{C_v}{C_p}$
C. C$_p$ - C$_v$
D. C$_p$ + C$_v$
Characteristics Gas Constant, \[R = C_p - C_v\]
Correct Answer: C
Solved Example: 72-5-08
The gas constant (R) is equal to the _________ of two specific heats.
A. Sum
B. Difference
C. Product
D. Ratio
Correct Answer: D
Solved Example: 72-5-09
The value of gas constant (R) for air in S. I. units is:
A. 0.287 J/kgK
B. 2.87 J/kgK
C. 28.7 J/kgK
D. 287 J/kgK
\[ R = \dfrac{\bar{R}}{\mathrm{mol.\ wt.}}\] \[ R = \dfrac{8314}{28.96} = 287.09\ J/KgK\]
Correct Answer: D
Solved Example: 72-5-10
When a perfect gas is heated at constant pressure from 15 $^\circ$C to 95$^\circ$ C, the heat required is 1136kJ/kg. When the same gas is heated at constant volume between the same temperatures the heat required is 808 kJ/kg. Calculate $\gamma$ for the gas.
A. 1.667
B. 1.405
C. 1.41
D. 1.29
Constant Volume Process \[Q = 808\ kJ/kg\] \[T_1 = 15 + 273 = 288\ K,\] \[T_2 = 95 + 293 = 368\ K,\] \[\Delta T = T_2 - T_1 = 80\ K \] \[Q = mC_v \Delta T, 806 = 1 \times C_v \times 80, C_v = 10.1\ KJ/kg K\] Constant Pressure Process \begin{align*} Q &= 1136\ KJ/kg\\ Q &= m C_p \Delta T\\ 1136 &= 1 \times C_p \times 80\\ C_p &= 14.2\ kJ/kg K \end{align*} \[\gamma = \dfrac{C_p}{C_v} = \dfrac{14.2}{10.1} = 1.405\]
Correct Answer: B
Solved Example: 72-5-11
A mono-atomic ideal gas ($\gamma$ = 1.67, molecular weight = 40 ) is compressed adiabatically from 0.1 MPa , 300 K to 0.2 MPa . The universal gas constant is 8.314 kJ/KmolK. The work of compression of the gas is:
A. 29.8
B. 19.9
C. 13.3
D. 0
Characteristic Gas Constant, \[ r = \dfrac{R}{M} = \dfrac{8.314}{40} = 0.208 kJ/kgK\] Using, \[\left(\dfrac{T_2}{T_1}\right) = \left(\dfrac{P_2}{P_1}\right)^{\dfrac{\gamma - 1}{\gamma}} \] \[ T_2 = 396.18K\] Work done in compression, \[= \dfrac{r(T_2 - T_1)}{\gamma - 1} = \dfrac{0.208 (396.18 - 300)}{1.67 - 1} = 29.8\]
Correct Answer: A
Solved Example: 72-5-12
5m$^3$ of air at 2 bar and 27$^\circ$C is compressed upto 6 bar. This process is governed by equation pV$^{1.3}$ = C. It is subsequently expanded to 2 bar. This process is reversible adiabatic. Find the net work in kJ:
A. -77.22 KJ
B. -81.09 KJ
C. -92.70 KJ
D. 102.41 KJ
Correct Answer: C
Polytropic Process
Learning Objectives:
- Calculate total work done in a polytropic process.
- Understand how different values of n give basic thermodynamic processes.
In a polytropic process both heat and work transfers take place. It follows the equation
where n is called the index of process or polytropic index.
Work done,
Change in internal energy, \[\Delta U = mC_v (T_2- T_1)\] Depending upon various values of n, there will be following cases:
- n = 0, constant pressure (Isobaric) process
- n = 1, constant temperature (Isothermal) process
- n = k, reversible adiabatic process
- n = $\infty$, constant volume (Isochoric) process
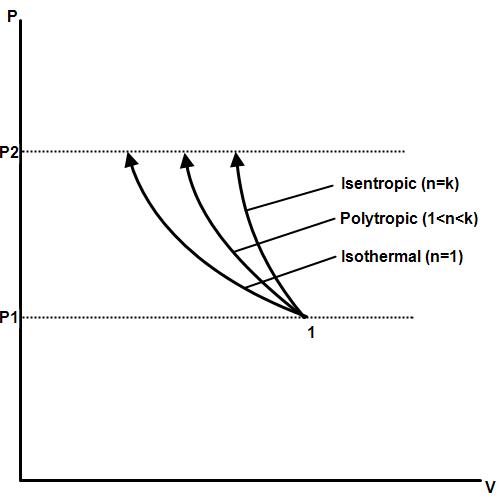
Tyler.neysmith, CC BY-SA 3.0, via Wikimedia Commons
Solved Example: 72-6-01
If the value of n = 0 in the equation pv$^n$ = C, then the process is called:
A. Constant volume process
B. Adiabatic process
C. Constant pressure process
D. Isothermal process
Correct Answer: C
Solved Example: 72-6-02
The value of n = 1 in the polytropic process indicates it to be:
A. Reversible process
B. Isothermal process
C. Adiabatic process
D. Irreversible process
When n= 1 in the equation PV$^n$ = constant, it reduces to PV = constant, which is Boyle's law where temperature is kept constant. Hence n=1 represents an isothermal process.
Correct Answer: B
Solved Example: 72-6-03
If value of n is infinitely large in a polytropic process pV$^n$ = C, then the process is known as constant:
A. Volume
B. Pressure
C. Temperature
D. Enthalpy
Correct Answer: A
Solved Example: 72-6-04
During polytropic process:
A. Heat transfer takes place across cylinder walls
B. Work is done
C. Steam may be wet, dry or superheated after expansion
D. All of the above
Correct Answer: D
Solved Example: 72-6-05
A fluid at 0.7 bar occupying 0.09 m$^3$ is compressed reversibly to a pressure of 3.5 bar according to pv$^n$ = constant. The fluid is then heated reversibly at constant volume until the pressure is 4 bar; the specific volume is then 0.5 m$^3$/kg. A reversible expansion according to the law pv$^{1.6}$ = constant restores the fluid to its initial state. Calculate the net work of the cycle.
A. 559 J
B. 565 J
C. 468 J
D. 522 J
Correct Answer: C
Solved Example: 72-6-06
A mass of gas at initial pressure of 30 bar, and with an internal energy of 1500kJ, is contained in a well-insulated cylinder of volume 0.1m$^3$. The gas is allowed to expand behind a piston until its internal energy is 1300 kJ, the law of expansion is pv$^2$ = constant. Calculate the final pressure.
A. 3.33 bar
B. 2.22 bar
C. 2.93 bar
D. 2.48 bar
Correct Answer: A
Solved Example: 72-6-07
A fluid at a pressure of 3 bar and with specific volume of 0.18m$^3$/kg, contained in a cylinder behind a piston expands reversibly to a pressure of 0.6 bar according to the law p = $\dfrac{C}{V^2}$, where C is a constant. The work done by the fluid on the piston is:
A. 29.84 KJ/kg
B. 32.11 KJ/kg
C. 35.76 KJ/kg
D. 38.03 KJ/kg
Correct Answer: A
Solved Example: 72-6-08
Properties of substances like pressure, temperature and density, in thermodynamic coordinates are:
A. Path functions
B. Point functions
C. Cyclic functions
D. Thermodynamic functions
Correct Answer: B
Solved Example: 72-6-09
Which of the following quantities is not the property of the system:
A. Pressure
B. Temperature
C. Specific volume
D. Heat
Correct Answer: D
Solved Example: 72-6-10
According to Avogadro's law, for a given pressure and temperature, each molecule of a gas:
A. Occupies volume proportional to its molecular weight
B. Occupies volume proportional to its specific weight
C. Occupies volume inversely proportional to its molecular weight
D. Occupies same volume
Correct Answer: D
Solved Example: 72-6-11
Which of the following is not the intensive property?
A. Pressure
B. Temperature
C. Density
D. Heat
An intensive property is a bulk property, meaning that it is a physical property of a system that does not depend on the system size or the amount of material in the system. Another way of looking at it is, if two containers having same pressure are combined the resultant pressure will remain same. The same can be stated regarding temperature and density. However, the heat content will be sum of two individual heat contents, hence it is not an intensive property.
Correct Answer: D
Solved Example: 72-6-12
Which of the following items is not a path function:
A. Heat
B. Work
C. Kinetic energy
D. Thermal conductivity
Correct Answer: D
Solved Example: 72-6-13
Heat and work are:
A. Point functions
B. Path functions
C. Intensive properties
D. Extensive properties
Correct Answer: B
Solved Example: 72-6-14
Which of the following parameters is constant for a mole for most of the gases at a given temperature and pressure:
A. Enthalpy
B. Volume
C. Mass
D. Entropy
Correct Answer: B
Solved Example: 72-6-15
For an ideal gas with constant values of specific heats, for calculation of the specific enthalpy:
A. It is sufficient to know only the temperature.
B. Both temperature and pressure are required to be known.
C. Both temperature and volume are required to be known.
D. Both temperature and mass are required to be known.
Correct Answer: A
Solved Example: 72-6-16
The area under the temperature-entropy curve (T-s curve) of any thermodynamic process represents:
A. Heat absorbed
B. Heat rejected
C. Either (A) or (B)
D. None of these.
Correct Answer: C
Solved Example: 72-6-17
A mixture of gas expands from 0.03 m$^3$ to 0.06 m$^3$ at a constant pressure of 1 MPa and absorbs 84 kJ of heat during the process. The change in internal energy of the mixture is:
A. 30 kJ
B. 54 kJ
C. 84 kJ
D. 114 kJ
Correct Answer: B
Solved Example: 72-6-18
Heating wet steam at constant temperature is heating it at constant:
A. Volume
B. Pressure
C. Entropy
D. Enthalpy
Correct Answer: B
Solved Example: 72-6-19
Intensive property of a system is one whose value:
A. Depends on the mass of the system, like volume
B. Does not depend on the mass of the system, like temperature, pressure, etc.
C. Is not dependent on the path followed but on the state
D. Is dependent on the path followed and not on the state
Correct Answer: B
Solved Example: 72-6-20
The index of compression n tends to reach ratio of specific heats $\gamma$ when:
A. Flow is uniform and steady
B. Process is isentropic
C. Process is isothermal
D. Process is isentropic and specific heat does not change with temperature
Correct Answer: D
Solved Example: 72-6-21
Change in enthalpy of a system is the heat supplied at:
A. Constant pressure
B. Constant temperature
C. Constant volume
D. Constant entropy
Correct Answer: A
Solved Example: 72-6-22
The term N.T.P. stands for:
A. Nominal temperature and pressure
B. Natural temperature and pressure
C. Normal temperature and pressure
D. Normal thermodynamic practice
Correct Answer: C
Solved Example: 72-6-23
In an isothermal process, the internal energy of gas molecules:
A. Increases
B. Decreases
C. Remains constant
D. May increase/decrease depending on the properties of gas
Correct Answer: C
Solved Example: 72-6-24
Work done is zero for the following process:
A. Constant volume
B. Free expansion
C. Throttling
D. All Of the above
Correct Answer: D
Solved Example: 72-6-25
In a non-flow reversible process for which p = (- 3V+ 15) $\times$ 10$^5$ N/m$^2$,V changes from 1 to 2 m$^3$. The work done will be about:
A. 100 $\times$ l0$^5$ joules
B. 1 $\times$ l0$^5$ joules
C. 10 $\times$ l0$^5$ joules
D. 10 $\times$ l0$^5$ kilo joules
Correct Answer: C
Solved Example: 72-6-26
In a free expansion process:
A. Work done is zero
B. Heat transfer is zero
C. Both (A) and (B) above
D. Work done is zero but heat increases
Correct Answer: C
Solved Example: 72-6-27
If a fluid expands suddenly into vacuum through an orifice of large dimension, then such a process is called:
A. Free expansion
B. Hyperbolic expansion
C. Adiabatic expansion
D. Parabolic expansion
Correct Answer: A
Solved Example: 72-6-28
Which of the following processes is irreversible process:
A. Isothermal
B. Adiabatic process
C. Throttling
D. All of the above
Correct Answer: C
Solved Example: 72-6-29
For a thermodynamic process to be reversible, the temperature difference between hot body and working substance should be:
A. Zero
B. Minimum
C. Maximum
D. Infinity
Correct Answer: A
Solved Example: 72-6-30
Minimum work in compressor is possible when the value of adiabatic index n is equal to:
A. 0.75
B. 1
C. 1.27
D. 1.35
Correct Answer: B
Solved Example: 72-6-31
A gas is compressed in a cylinder by a movable piston to a volume one-half its original volume. During the process 300 kJ heat left the gas and internal energy remained same. The work done on gas in Nm will be:
A. 300 Nm
B. 300,000 Nm
C. 30 Nm
D. 3000 Nm
Correct Answer: B
Solved Example: 72-6-32
For reversible adiabatic process, change in entropy is:
A. Maximum
B. Minimum
C. Zero
D. Unpredictable
Correct Answer: C
Solved Example: 72-6-33
Change in enthalpy in a closed system is equal to heat transferred if the reversible process takes place at constant:
A. Pressure
B. Temperature
C. Volume
D. Internal energy
Correct Answer: A
Cyclic Process
Learning Objectives:
- To be able to identify and describe energy exchange processes (in terms of various forms of energy, heat and work) in various systems.
- To be able to explain how various heat engines work (e.g. a refrigerator, an IC engine,a jet engine).
- To be able to apply the steady-flow energy equation or the First Law of Thermodynamics to a system of thermodynamic components (heaters, coolers, pumps, turbines, pistons, etc.) to estimate required balances of heat, work and energy flow.
- To be able to explain the concepts of path dependence/independence and reversibility/ irreversibility of various thermodynamic processes, to represent these in terms of changes in thermodynamic state.
- To be able to apply ideal cycle analysis to simple heat engine cycles to estimate thermal efficiency and work as a function of pressures and temperatures at various points in the cycle.
A cyclic process is one that periodically returns to its initial state. Change of a state function in one cycle is zero. Therefore, change in internal energy \(\Delta\) U = 0.
By applying the first law of thermodynamics, \[Q = W\] Cyclic equilibrium processes are represented by closed lines in state space. Work done during one cycle will be the area enclosed in the closed region which represents that cyclic process.
Efficiency in Cyclic Processes:
\[\eta = \dfrac{\mathrm{Work\ Done}}{\mathrm{Heat\ Absorbed}}\]
Solved Example: 72-7-01
A fluid at 0.7 bar occupying 0.09 $m^3$ is compressed reversibly to a pressure of 3.5 bar according to $pv^n$ = constant. The fluid is then heated reversibly at constant volume until the pressure is 4 bar; the specific volume is then 0.5 $m^3/kg$. A reversible expansion according to the law $pv^{1.6}$ = constant restores the fluid to its initial state. Calculate the net work of the cycle.
A. 559 J
B. 565 J
C. 468 J
D. 669.44
First, consider process 3 $\rightarrow$ 1: \begin{align*} P_{1}V_{1}^{1.6}&=P_{3}V_{3}^{1.6}\\ \left( \dfrac {V_{3}}{V_{1}}\right) ^{1.6}&=\left( \dfrac {P_{1}}{P_{3}}\right) \\ V_{3}&=\left( \dfrac {0.7}{4}\right) ^{\dfrac {1}{1.6}}\times 0.09 =0.0303\ m^{3}\\ \end{align*} Now, consider process 2 $\rightarrow$ 3: \[V_{2}=V_{3}=0.0303\ m^{3}\] Now, consider process 1 $\rightarrow$ 2: \begin{align*} P_{1}V_{1}^{n}&=P_{2}V_{2}^{n}\\ n=\dfrac {\ln \left( \dfrac {P_{1}}{P_{2}}\right) }{\ln \left( \dfrac {V_{2}}{V_{1}}\right) }&=\dfrac {\ln \left( \dfrac {0.7}{3.5}\right) }{\ln \left( \dfrac {0.0303}{0.09}\right) }\\ n &=1.48 \end{align*} \begin{align*} W_{1\rightarrow 2}&=\int ^{V_{2}}_{V_{1}}PdV \\ &=\int ^{V_{2}}_{V_{1}}\dfrac {C}{V^{n}}dV \\ &=C\int ^{0.0303}_{0.09}V^{-n}dV \\ &=-9008.15\ J \end{align*} \[W_{3\rightarrow 1} =\int ^{0.09}_{0.0303}PdV =9677.59\ J\] \begin{align*} W_{net} &=W_{1\rightarrow 2} + W_{2\rightarrow 3} + W_{3\rightarrow 1} \\&=-9008.15 + 0 + 9677.59 \\&=669.44\ J \end{align*}
Correct Answer: D
Solved Example: 72-7-02
A perfect heat engine works on Carnot Cycle between 1000 Deg. C and 200 Deg. C. The efficiency of the engine will be:
A. 80%
B. 60%
C. 37.2%
D. 62.8%
$T_1 = 1000 + 273 = 1273\ K, T_2 = 200 + 273 = 473\ K$
Efficiency of Carnot cycle is given by:
\[\eta = 1 - \dfrac{T_1}{T_2} = 1 - \dfrac{473}{1273} = 0.628\]
Correct Answer: D
Solved Example: 72-7-03
In order that a cycle be reversible, following must be satisfied.
A. Free expansion or friction resisted expansion/compression process should not be encountered
B. When heat is being absorbed, temperature of hot source and working substance should be same
C. When heat is being rejected, temperature of cold source and working substance should be same
D. All of the above.
Correct Answer: D
Solved Example: 72-7-04
Thermal power plant works on:
A. Carnot cycle
B. Joule cycle
C. Rankine cycle
D. Otto cycle
Correct Answer: C
Solved Example: 72-7-05
Which of the following is an irreversible cycle?
A. Carnot
B. Stirling
C. Ericsson
D. None of the above.
Correct Answer: D
Solved Example: 72-7-06
Otto cycle consists of following four processes:
A. Two isothermals and two isentropics
B. Two isentropics and two constant volumes
C. Two isentropics, one constant volume and one constant pressure
D. Two isentropics and two constant pressures
Correct Answer: B
Solved Example: 72-7-07
The efficiency of a Carnot engine depends on:
A. Working substance
B. Design of engine
C. Size of engine
D. Temperatures of source and sink
\[\eta = 1 - \dfrac{T_L}{T_H}\] So the efficiency depends only upon the temperature of higher temp. reservoir and lower temp. reservoir. Also, unline other cycles, it is independent of properties of working medium.
Correct Answer: D
Solved Example: 72-7-08
For same compression ratio and for same heat added:
A. Otto cycle is more efficient than Diesel cycle
B. Diesel cycle is more efficient than Otto cycle
C. Efficiency depends on other factors
D. Both Otto and Diesel cycles are equally efficient
Correct Answer: A
Solved Example: 72-7-09
The efficiency of Carnot cycle is maximum for:
A. Gas engine
B. Petrol engine
C. Steam engine
D. Reversible engine
Correct Answer: D
Solved Example: 72-7-10
Carnot cycle is:
A. A reversible cycle
B. An irreversible cycle
C. A semi-reversible cycle
D. A quasi static cycle
Correct Answer: A
Solved Example: 72-7-11
Diesel cycle consists of following four processes:
A. Two isothermals and two isentropics
B. Two isentropics, and two isochorics.
C. Two isentropics, one isochoric and one isobaric
D. Two isentropics and two isobaric
Correct Answer: C
Solved Example: 72-7-12
If both Stirling and Carnot cycles operate within the same temperature limits, then efficiency of Stirling cycle as compared to Carnot cycle:
A. More
B. Less
C. Equal
D. Depends on other factors
Correct Answer: C
Solved Example: 72-7-13
Stirling and Ericsson cycles are:
A. Reversible cycles
B. Irreversible cycles
C. Quasi-static cycles
D. Semi-reversible cycles
Correct Answer: A
Solved Example: 72-7-14
A cycle consisting of two adiabatics and two constant pressure processes is known as:
A. Otto cycle
B. Ericsson cycle
C. Joule cycle
D. Stirling cycle
Correct Answer: C
Solved Example: 72-7-15
Reversed Joule cycle is called:
A. Carnot cycle
B. Rankine cycle
C. Brayton cycle
D. Bell Coleman cycle
Correct Answer: C
Solved Example: 72-7-16
Brayton cycle consists of following four processes:
A. Two isothermals and two isentropics
B. Two isentropics and two isochoric
C. Two isentropics, one isochoric and one isobaric
D. Two isentropics and two isobaric
Correct Answer: D
Solved Example: 72-7-17
The cycle in which heat is supplied at constant volume and rejected at constant pressure is known as:
A. Dual combustion cycle
B. Diesel cycle
C. Atkinson cycle
D. Rankine cycle
Correct Answer: C
Solved Example: 72-7-18
The efficiency of Diesel cycle with decrease in cut off:
A. Increases
B. Decreases
C. Remains unaffected
D. First increases and then decreases
Correct Answer: A
Solved Example: 72-7-19
Which of the following cycles has maximum efficiency:
A. Rankine
B. Stirling
C. Carnot
D. Brayton
Among all power cycles, Canot cycle has the higherst thermal efficiency.
Correct Answer: C
Solved Example: 72-7-20
The ideal efficiency of a Brayton cycle without regeneration with increase in pressure ratio will:
A. Increases
B. Decreases
C. Remain unchanged
D. Increase/decrease depending on application
Correct Answer: A
Solved Example: 72-7-21
The ideal efficiency of a Brayton cycle with regeneration, with increase in pressure ratio will:
A. Increase
B. Decrease
C. Remain unchanged
D. Increase/decrease depending on application
Correct Answer: B
Solved Example: 72-7-22
The following cycle is used for air craft refrigeration:
A. Joule cycle
B. Carnot cycle
C. Bell-Coleman cycle
D. Reversed-Brayton cycle.
Correct Answer: D
Solved Example: 72-7-23
Gas turbine cycle consists of:
A. Two isothermals and two isentropics
B. Two isentropics and two constant volumes
C. Two isentropics, one constant volume and one constant pressure
D. Two isentropics and two constant pressures
Correct Answer: D
Solved Example: 72-7-24
The thermodynamic difference between a Rankine cycle working with saturated steam and the Carnot cycle is that:
A. Carnot cycle can't work with saturated steam
B. Heat is supplied to water at temperature below the maximum temperature of the cycle
C. A Rankine cycle receives heat at two places
D. Rankine cycle is hypothetical
Correct Answer: B