Learning Objectives:

• State the air-standard assumptions and the cold-air-standard assumptions.

• Know the terms regarding reciprocating engines like TDC, BDC, clearance volume,compression ratio, and mean effective pressure.

• Understand that mean effective pressure is a parameter used to compare the performances of reciprocating engines of equal size.

• Draw the P-v and T-s diagrams for Otto, Diesel, and dual combustion cycles.

• Solve the numerical calculating the thermal efficiency, amount of heat transfer, mean effective pressure, and the highest temperature and pressure in the cycles (Otto, dual) assuming constant specific heats.

• Appreciate that the thermal efficiency of ideal Otto cycle is a function of compression ratio and specific heat ratios.

Classification of Cycles: The purpose of a thermodynamic cycle is either to produce power, or to produce refrigeration/pumping of heat. Therefore, the cycles are broadly classified as follows:

1. Heat engine or power cycles.

2. Refrigeration/heat pump cycles.

Any thermodynamic cycle is essentially a closed cycle in which, the working substance undergoes a series of processes and is always brought back to the initial state.
However, some of the power cycles operate on open cycle. It means that the working substance is taken into the unit from the atmosphere at one end and is discharged into the atmosphere after undergoing a series of processes at the other end. The following are illustrations of heat engines operating on open cycle: Petrol and diesel engines in which the air and fuel are taken into the engine from a fuel tank and products of combustion are exhausted into the atmosphere.
(ii) Steam locomotives in which the water is taken in the boiler from a tank and steam is exhausted into the atmosphere. Essentially, such devices do not form a cycle. However, they can be analyzed by adding an imaginary processes to bring the state of the working substance, thus completing a cyclic. Note that the terms closed cycle and open cycle used here do not mean closed system cycle and open system cycle. In fact, the processes both in closed and open cycles could either be closed or open system processes.
Different types of working fluids are employed in the power plants. The nature of the working fluids can be classified into two groups: vapours and gases. The power cycles are accordingly classified into two groups as:

1. Vapor power cycles in which the working fluid undergoes a phase change during the cyclic process.

2. Gas power cycles in which the working fluid does not undergo any phase change.

In the thermodynamic analysis of power cycles, our chief interest lies in estimating the energy conversion efficiency or the thermal efficiency. The thermal efficiency of a heat engine is defined as the ratio of the network delivered to the energy absorbed as heat.

Analysis of Cycles: In air standard analysis, air is considered as the working medium. The analysis is carried out with the following assumptions.

1. The working substance consists of a fixed mass of air and behaves as a perfect gas. The closed system is considered which under goes a cycle process. Therefore, there are no intake or exhaust process.

2. The combustion process is replaced by an equivalent heat addition process form an external source. Thus there is no change in the chemical equilibrium of the working fluid and also composition.

3. There is no exhaust process; this is replaced by an equivalent heat rejection process.

4. Compression and expansion processes in the cycle are considered as reversible adiabatic process.

5. The specific heats \(C_p\) and \(C_v\) of air do not vary with temperature.

Solved Example: 74-1-01

The work output from the turbine in a Rankine cycle is given by the change of _____ between inlet and outlet.(UPRVUNL AE ME July 2021)

A. Temperature

B. Entropy

C. Internal energy

D. Enthalpy

Correct Answer: D

Learning Objectives:

• State and explain Carnot’s theorem.

Assume the Carnot cycle is being performed on an ideal gas.

T-s Diagram

We start the gas at some point 1, which corresponds to an initial condition \(T_h\) and \(s_h\) and perform a series of operations on the gas that move its state around a rectangle in T - s space.

Isothermal Expansion

The first process in the Carnot cycle is an isothermal expansion, which corresponds to a vertical line in T-s space. The gas is at \(T_h\) and is brought into contact with a thermal reservoir. The volume of the gas is then increased while it is in contact with the reservoir.

Isentropic Expansion

The second process in the Carnot cycle is an isentropic expansion in which the heat reservoir is removed and the gas is allowed to expand with no input of heat . The temperature falls as the gas expands, but the entropy is fixed, since no heat is transferred to the gas. This process corresponds to a horizontal line at \(\tau_h\) in \(\tau - \sigma\) space traversed to the left.

Isothermal Compression

The third process in the Carnot cycle is a compression is then compressed at temperature \(T_l\) in contact with a heat reservoir. This isothermal compression corresponds to a vertical line at \(s_l\) traversed in the negative direction.

Isentropic Compression

Finally, the gas is compressed back to its initial volume. The gas is no longer in contact with a heat reservoir, so T increases, and the process corresponds to a horizontal path traversed to the right at entropy \(s_1\).

Work Done

Since the system returns to its initial state after a cycle, the total change in energy over this cycle is 0. \[\begin{aligned} 0 = \oint dU &= \oint \tau d\sigma - \underbrace{\oint pdV}_{W \text{ by gas}}\\ W\text{ by gas} &= \oint \tau d\sigma\\ &= \text{ area of rectangle}\\ &= \left( T_{h} - T_{l} \right)\left( s_{h} - s_{l} \right)\end{aligned}\]

P-V Diagram:

We calculate the work done over a single Carnot cycle. The analysis is now performed in terms of the pressure p and the volume V of the gas.

Isothermal Expansion:

The work done by the gas in going from points 1 to 2 is,

\[\begin{aligned} W_{1 \rightarrow 2} = +\int_{V_{1}}^{V_{2}}pdV\end{aligned}\]

Note: The integral is positive because we are finding the work performed by the gas.
Since the process is carried out on an ideal gas, use the ideal gas relation to remove p from the integral,

\[\begin{aligned} W_{1 \rightarrow 2} = N\tau_{h}\int_{V_{1}}^{V_{2}}dV = N\tau_{h}\ln\left( \frac{V_{2}}{V_{1}} \right)\end{aligned}\]

Since \(\Delta\) U = 0 for an isothermal process, all of this work must come from the heat taken up by the gas. \[\begin{aligned} W_{1 \rightarrow 2} = Q_{1}\end{aligned}\]

Isentropic Expansion:

\[\begin{aligned} W_{2 \rightarrow 3} = U(\tau_{h}) - U(\tau_{l}) = \frac{3}{2}N\left( \tau_{h} - \tau_{l} \right)\end{aligned}\]

Compression Processes:

\[\begin{aligned} W_{3 \rightarrow 4} &= N\tau_{l}\log \frac{V_{4}}{V_{3}} = Q_{2}\\ W_{4 \rightarrow 1} &= U(\tau_{l}) - U(\tau_{h})\\ &= -\frac{3}{2}N\tau\log(\tau_{h} - \tau_{l})\end{aligned}\]

Total Work:

The total work done by the gas is: \[\begin{aligned} W_{1 \rightarrow 2} + W_{2 \rightarrow 3} + W_{3 \rightarrow 4} + W_{4 \rightarrow 1} = W_{1 \rightarrow 2} + W_{3 \rightarrow 4}\end{aligned}\]

\(W_{4 \rightarrow 1}\) is equal and opposite to the work done by the gas during the isentropic expansion. Only the isothermal processes contribute to the work done by the gas, since only when heat is transferred is work done.

We would like to express the result in terms of \(V_{1}\) and \(V_{2}\) only. Using the fact that the gas undergoes an adiabatic expansion,

\[\begin{aligned} \tau V^{\frac{2}{3}} &= \text{ constant}\\ \tau_{h}V_{2}^{\frac{2}{3}} &= \tau_{l}V_{3}^{\frac{2}{3}}\\ \Rightarrow \frac{V_{3}}{V_{2}} &= \left( \frac{\tau_{h}}{\tau_{l}} \right)^{\frac{3}{2}}\end{aligned}\]

Also, from the adiabatic compression, \[\begin{aligned} \tau_{l}V_{4}^{\frac{2}{3}} &= \tau_{h}V_{1}^{\frac{2}{3}}\end{aligned}\] Combining these results, \[\begin{aligned} \frac{V_{4}}{V_{1}} &= \left( \frac{\tau_{h}}{\tau_{l}} \right)^{\frac{3}{2}} = \frac{V_{3}}{V_{2}}\\ \frac{V_{4}}{V_{3}} &= \frac{V_{1}}{V_{2}}\\ \Rightarrow \log\left( \frac{V_{4}}{V_{3}} \right) &= \log\left( \frac{V_{1}}{V_{2}} \right)\\ &= -\log\left( \frac{V_{2}}{V_{1}} \right)\end{aligned}\]

The work done by the gas can then be written, \[\begin{aligned} W \text{ by gas} &= N\tau_{h}\log \left( \frac{V_{2}}{V_{1}} \right) - N\tau_{l}\log \left( \frac{V_{2}}{V_{1}} \right)\\ &= N(\tau_{h} - \tau_{l})\log\left( \frac{V_{2}}{V_{1}} \right)\end{aligned}\]

Efficiency:

\[\begin{aligned} \eta &= \frac{W}{Q_{1}} = \frac{N(\tau_{h} - \tau_{l})\log\left( \frac{V_{2}}{V_{1}} \right)}{N\tau_{h}\log\left( \frac{V_{2}}{V_{1}} \right)}\\ &= \frac{\tau_{h} - \tau_{l}}{\tau_{h}} = \eta_{c}\end{aligned}\]

• We have recovered the Carnot efficiency by examining an actual cycle. Thus our model heat engine is an example of an ideal heat engine.

• All heal heat engines operate on this same basic process, although they included many inefficiencies.

• Doing this same analysis in the opposite direction would be analogous to the operation of a refrigerator.

Solved Example: 74-2-01

100% efficiency of a thermal cycle cannot be achieved because of:

A. Frictional losses

B. It is not possible to achieve 0$^\circ$K temperature

C. Leakage

D. Non-availability of ideal substance

Correct Answer: B

Solved Example: 74-2-02

A Carnot refrigerator has a lower temp. of 5$^\circ$C and rejects heat to the surround at 27$^\circ$C. If the lower temp. is decreased to -13$^\circ$C, while the surrounding temp. remains same, calculate ratio of the increase of the input work for the same heat absorbed from the cold reservoir.

A. 0.95

B. 0.76

C. 0.88

D. 0.98

Correct Answer: A

Solved Example: 74-2-03

During which of the following process does heat rejection takes place in Carnot cycle?

A. Isothermal expansion

B. Isentropic expansion

C. Isothermal compression

D. Isentropic compression

Correct Answer: C

Solved Example: 74-2-04

Which is the incorrect statement about Carnot cycle?

A. It is used as the alternate standard of comparison of all heat engines.

B. All the heat engines are based on Carnot cycle.

C. It provides concept of maximizing work output between the two temperature limits.

D. All of the above.

Correct Answer: B

Solved Example: 74-2-05

Efficiency of a Carnot engine is given as 80%. If the cycle direction be reversed, what will be the value of COP of reversed Carnot cycle: (ISRO Scientist ME 2013)

A. 1.25

B. 0.8

C. 0.5

D. 0.25

Efficiency of Carnot heat engine \begin{align*} \eta &=\dfrac {T_{1}-T_{2}}{T_{1}}\\ 0.8 &=\dfrac {T_{1}-T_{2}}{T_{1}}\\ 0.8T_{1} &=T_{1}-T_{2} \end{align*} In the case of reversed heat engine, \[COP =\dfrac {T_{1}}{T_{1}-T_{2}}= \dfrac {T_{1}}{0.8T_{1}} =\dfrac {1}{0.8} =1.25\]

Correct Answer: A

Learning Objectives:

• To analyze ideal and actual Rankine Power cycle.

• Give the steps in an ideal and actual Rankine Cycle and draw the corresponding T-s and P-v diagrams.

• Use conservation of energy and the appropriate property relations to calculate the heat transfer and work in/out of each step of an Rankine Cycle as well as to calculate the cycle efficiency.

Ideal Rankine Cycle:

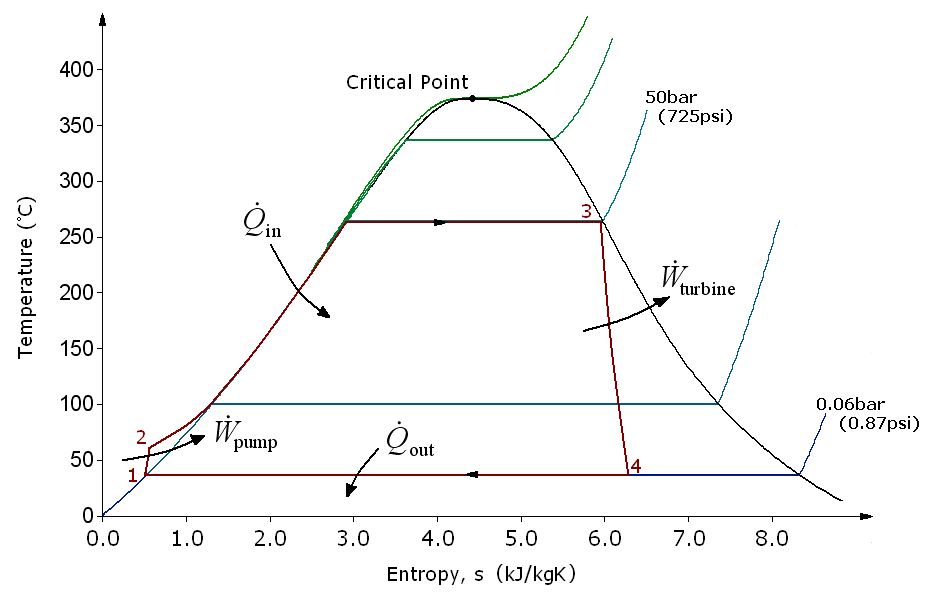
There are four processes in the Rankine cycle. These states are identified by numbers (in brown) in the above T-s diagram.

• Process 1-2: The working fluid is pumped from low to high pressure. As the fluid is a liquid at this stage, the pump requires little input energy.

• Process 2-3: The high pressure liquid enters a boiler where it is heated at constant pressure by an external heat source to become a dry saturated vapour. The input energy required can be easily calculated graphically, using an enthalpy-entropy chart , or numerically, using steam tables.

• Process 3-4: The dry saturated vapour expands through a turbine, generating power. This decreases the temperature and pressure of the vapour, and some condensation may occur. The output in this process can be easily calculated using the chart or tables noted above.

• Process 4-1: The wet vapour then enters a condenser where it is condensed at a constant pressure to become a saturated liquid.

Work done on pump, per kg of water, \(W_P= h_2-h_1\)
Energy added in steam generator, \(q_1= h_3-h_2\)
Work delivered by turbine, \(WT= h_3-h_4\)
Energy rejected in the condenser, \(q_2= h_4-h_1\)

Practical Rankine Cycle:

Pump and Turbine do not operate isentropically in practice. The practical Rankine cycle is shown as 1-2 -3-4-1. In the actual turbine, the work delivered is less than the isentropic turbine. Similarly, the work consumed by an actual pump is greater than the work consumed by an isentropic pump. That is, \[h_3-h_4 < h_3-h_4\] \[h_2 -h_1 > h_2-h_1\] Thermal efficiency of a practical Rankine cycle,

The performance of an actual turbine or pump is usually expressed in terms of isentropic efficiency. Isentropic efficiency of turbine is defined as the ratio of Work delivered by actual turbine to Work delivered by an isentropic turbine.

Solved Example: 74-3-01

Rankine efficiency of a Steam Power Plant

A. Improves in Summer as compared to that in Winter

B. Improves in Winter as compared to that in Summer

C. Is unaffected by climatic conditions

D. None of the mentioned

In winters, temperature of cooling water is low, which increases Condenser’s efficiency.

Correct Answer: B

Solved Example: 74-3-02

Rankine cycle comprises of:

A. Two isentropic and two isochoric processes

B. Two isentropic and two isobaric processes

C. Two isothermal and two isobaric processes

D. None of the mentioned

Rankine cycle is a reversible cycle which have two constant pressure and two constant temperature processes.

Correct Answer: B

Solved Example: 74-3-03

In Rankine cycle, the work output from the turbine is given by:

A. Change of internal energy between inlet and outlet

B. Change of enthalpy between inlet and outlet

C. Change of entropy between inlet and outlet

D. Change of temperature between inlet and outlet

Work output(turbine) = $h_1-h_2$

Correct Answer: B

Solved Example: 74-3-04

Which of the following contributes to the improvement of efficiency of Rankine cycle in a Thermal Power Plant?

A. Reheating of steam at intermediate stage

B. Regeneration use of steam for heating Boiler feed water

C. Use of high pressures

D. All of the mentioned

The regenerative features effectively raise the nominal cycle heat input temperature, by reducing the addition of heat from the Boiler/fuel source at the relatively low feedwater temperatures that would exist without regenerative feedwater heating.

Correct Answer: D

Solved Example: 74-3-05

A simple Rankine cycle operates the Boiler at 3 MPa with an outlet temperature of 350$^\circ$C and the Condenser at 50 kPa. Assuming ideal operation and processes, what is the thermal efficiency of this cycle?

A. 7.7

B. 17.7

C. 27.7

D. 37.7

Fixing the states: \begin{align*} h_1 &= 340.5\ kJ/kg,\\ h_2 &= h_1 + v_1 (P_2 - P_1) = 343.5\ kJ/kg,\\ h_3 &= 3115.3\ kJ/kg,\\ s_3 &= 6.7428\ kJ/kg K,\\ x_4 &= 0.869,\\ h_4 &= 2343.9\ kJ/kg \end{align*} \[\eta = 1 - Q_{out} / Q_{in} = 1 - (h_4 - h_1) / (h_3 - h_2) = 27.7\%\]

Correct Answer: C

Solved Example: 74-3-06

In a Rankine cycle, the maximum pressure of steam supplied is 6 bar. The dryness fraction is 0.9. The exhaust pressure is 0.7 bar. Find efficiency of Rankine cycle.

A. 13.4%

B. 24.6%

C. 27.9%

D. 35.1%

\[h_{1}=h_{g} \bigg|_{0.6\ MPa}=2756\ \mathrm{kJ/kg}\] \[h_{3}=h_{f} \bigg|_{0.07\ MPa}=376.92\ \mathrm{kJ/kg}\] \begin{align*} h_{2} &=h_{3}+x\ h_{fg}\\ &=376.92+5.9\left( 2283\right)\\ &=2431.7\ \mathrm{kJ/kg} \end{align*} \begin{align*} \mathrm{Pump\ Work} &=v_{f}\left( \Delta P\right)\\ &=0.001\left( 6\times 10^{5}-0.7\times 10^{5}\right)\\ &= 5.3\ \mathrm{kJ/kg} \end{align*} \[h_{4} = h_{3} + \mathrm{Pump\ Work} = 376.92+5.3 = 382.1\ \mathrm{kJ/kg}\] \[\mathrm{Net\ work} =\mathrm{Turbine\ work}-\mathrm{Pump\ work}\] \[\mathrm{Net\ work} =324.3-5.3 =318\ \mathrm{kJ/kg}\] \[\mathrm{Heat\ supplied}=h_{1}-h_{4} =2756-382.1 =2373.9\ \mathrm{kJ/kg}\] \[\eta =\dfrac{318}{2373}=13.4\% \]

Correct Answer: A

Learning Objectives:

• Give the steps in an ideal Otto Cycle and draw the corresponding T-s and P-v diagrams. Used conservation of energy and the appropriate property relations to calculate the heat transfer and work in/out of each step of an Otto Cycle as well as to calculate the cycle efficiency.

Otto cycle is a gas power cycle that is used in spark-ignition internal combustion engines (modern petrol engines).
An Otto cycle consists of four processes:

• Two isentropic (reversible adiabatic) processes

• Two isochoric (constant volume) processes

• Process 1-2: Isentropic compression In this process, the piston moves from bottom dead centre (BDC) to top dead centre (TDC) position. Air undergoes reversible adiabatic (isentropic) compression. We know that compression is a process in which volume decreases and pressure increases. Hence, in this process, volume of air decreases from V\(_1\) to V\(_2\) and pressure increases from p\(_1\) to p\(_2\). Temperature increases from T\(_1\) to T\(_2\). As this an isentropic process, entropy remains constant (i.e., s\(_1\)=s\(_2\)). Refer p-V and T-s diagrams for better understanding.

• Process 2-3: Constant Volume Heat Addition: Process 2-3 is isochoric (constant volume) heat addition process. Here, piston remains at top dead centre for a moment. Heat is added at constant volume (V\(_2\) = V\(_3\)) from an external heat source. Temperature increases from T\(_2\) to T\(_3\), pressure increases from p\(_2\) to p\(_3\) and entropy increases from s\(_2\) to s\(_3\). (See p-V and T-s diagrams above).

• Process 3-4: Isentropic expansion In this process, air undergoes isentropic (reversible adiabatic) expansion. The piston is pushed from top dead centre (TDC) to bottom dead centre (BDC) position. Here, pressure decreases fro p\(_3\) to p\(_4\), volume rises from v\(_3\) to v\(_4\), temperature falls from T\(_3\) to T\(_4\) and entropy remains constant (s\(_3\)=s\(_4\)). (Refer p-V and T-s diagrams above).

• Process 4-1: Constant Volume Heat Rejection The piston rests at BDC for a moment and heat is rejected at constant volume (V\(_4\)=V\(_1\)). In this process, pressure falls from p\(_4\) to p\(_1\), temperature decreases from T\(_4\) to T\(_1\) and entropy falls from s\(_4\) to s\(_1\). (See diagram above).

  In process 4-1,

  Heat Rejected = \[m C_v(T_4 - T_1)\]

Solved Example: 74-4-01

Otto cycle efficiency is higher than Diesel cycle efficiency for the same compression ratio and heat input because in Otto cycle:

A. Combustion is at constant volume

B. Expansion and compression are isentropic

C. Maximum temperature is higher

D. Heat rejection is lower

Correct Answer: D