Electrical Fundamentals
Coulomb's Law
Learning Objectives:
- Define charge and Coulomb's law.
- Explain the force of attraction between two charged bodies as a vector quantity.
Solved Example: 18-1-01
The electrical charge associated with one electron, in Coulombs, is:
A. 1
B. -1
C. 6.25 $\times 10^{18}$
D. -1.60 $\times 10^{-19}$
The elementary charge, usually denoted as e or sometimes q, is the electric charge carried by a single proton, or equivalently, the magnitude of the electric charge carried by a single electron, which has charge -e. This value is constant and equals to (-)1.6$ \times 10^{-19}$ Coulombs.
Correct Answer: D
Solved Example: 18-1-02
Two identical point charges with mass $m_1$ = $m_2$ = 0.60 grams are suspended in air with strings of length = 250mm. The total angle between them is 15$^\circ$. The charge each of them carrying is:
A. 19.15 nC
B. 27.45 nC
C. 31.87 nC
D. 12.11 nC
Equating horizontal components $T\sin 7.5^{\circ }=k\dfrac {q_{1}q_{2}}{r^{2}}$
Equating vertical components $T\cos 7.5^{\circ }=mg$
Dividing above two equations, \[\tan 7.5^{\circ }=k\dfrac {q^{2}}{r^{2}mg}\] \[q^{2}=\dfrac {r^{2}mg\tan 7.5^{\circ }}{k}\] where, \[r=2\times 250\times \sin 7.5^{\circ } =65.26\ \mathrm{mm}\] \[q=1.915\times 10^{-8}C=19.15\ \mathrm{nC}\]
Correct Answer: A
Solved Example: 18-1-03
Four charges are arranged in a square with sides of length 2.5 cm. The two charges in the top right and bottom left corners are +3.0 $\times$ 10$^{-6}$ C. The charges in the other two corners are -3.0 $\times$ 10$^{-6}$ C. What is the net force exerted on the charge in the top right corner by the other three charges?
A. 68.7 N
B. 72.9 N
C. 88.2 N
D. 118.0 N
\[F = \dfrac{kq_1q_2}{r^2}\] \begin{align*} F_{14} = F_{12} &= \dfrac{(9\times 10^{9})(3\times 10^{-6})(3\times 10^{-6})}{(0.025)^2} = 129.5\ N \end{align*}
(F$_{12}$ towards q$_2$ and F$_{14}$ towards q$_4$)
\begin{align*} F_{13} &= \dfrac{(9\times 10^{9})(3\times 10^{-6})(3\times 10^{-6})}{(0.025\sqrt{2})^2}\\ &= 64.7\ N\ (\mathrm{away\ from}\ q_3\ \mathrm{as\ shown}) \end{align*}Correct Answer: D
Solved Example: 18-1-04
Three charges 4q, Q and q are in a straight line in the position of 0, $\dfrac{l}{2}$ and l respectively. The resultant force on q will be zero, if Q=?
A. -q
B. -2q
C. -q$^2$
D. 4q
The force between Q and q ${{F}_{2}}=\dfrac{1}{4\pi {{\varepsilon}_{0}}}\cdot \dfrac{Q\times q}{{{\left(\dfrac{l}{2}\right)}^{2}}}$
Since, the resultant force must be zero, \begin{align*} {{F}_{1}}+{{F}_{2}}&=0\\ \dfrac{4{{q}^{2}}}{{{l}^{2}}}&=-\dfrac{4Qq}{{{l}^{2}}}\\ Q&=-q \end{align*}
Correct Answer: A
Solved Example: 18-1-05
Two charges of + 4 $\mu$C and -16 $\mu$C are separated from each other by a distance of 0.6 m. At what distance should a third charge of + 6 $\mu$C be placed from + 4 $\mu$C so that no force exerts on it will be zero?
A. 0.4 m
B. 0.6 m
C. 1.2 m
D. 0.3 m
\begin{align*} k\dfrac{q_{A}q_{c}}{d^{2}} &=k\dfrac{q_{B}q_{c}}{\left(0.6 + d\right) ^{2}}\\ \dfrac{24}{d^{2}} &=\dfrac{96}{\left(0.6 + d\right) ^{2}}\\ 4d^{2} &=0.36+1.2d+d^{2}\\ 3d^{2}-1.2d-0.36 &=0\\ d &=0.6\ m \end{align*}
Correct Answer: B
Solved Example: 18-1-06
The electrostatic force between two charges $q_1$ and $q_2$ is given by:
A. Newton's law
B. Coulomb's law
C. Faraday's law
D. Ampere's law
Correct Answer: B
Solved Example: 18-1-07
The force between two charges is 200 N. If the distance between the charges is doubled, the force will be _______.
A. 400 N
B. 100 N
C. 50 N
D. 200 N
The electrostatic force between two charges is inversely proportional to the square of distance between charges. If the distance is doubled, then the force will become one-fourth.
Correct Answer: C
Solved Example: 34534
If the distance between two charges is doubled, the force between them:
A. Halves
B. Doubles
C. Quadruples
D. Decreases by a factor of four
Correct Answer: D
Solved Example: 456456
Which of the following is true according to Coulomb's Law?
A. Like charges attract each other.
B. Opposite charges repel each other.
C. The force is proportional to the product of the charges.
D. The force is independent of distance.
Correct Answer: C
Solved Example: 567567
What does Coulomb's Law describe?
A. The relationship between electric fields and current
B. The force between two charged objects
C. The potential energy in a circuit
D. The behavior of magnets
Correct Answer: B
Electrostatic Field
Learning Objectives:
- Define electrostatic field in terms of given charge at a given distance.
Solved Example: 2342345
The energy stored in an electric field is determined by:
A. Electric field strength only
B. Charge only
C. Both electric field strength and volume
D. None of the above
Correct Answer: C
Solved Example: 345345
Which of the following is true about equipotential surfaces?
A. They are always flat
B. No work is done moving a charge along an equipotential surface
C. They can intersect
D. They are parallel to electric field lines
Correct Answer: B
Solved Example: 9418-01
The electric field strength of a charge:
A. Increases with distance
B. Decreases with cube of distance
C. Decreases with distance
D. Decreases with square of distance
Correct Answer: D
Solved Example: 9418-02
Electric flux is a _______ field, and its density is a _______ field.
A. Vector, vector
B. Scalar, vector
C. Vector, scalar
D. Scalar, scalar
Correct Answer: B
Solved Example: 9418-03
What is the unit of Electric field intensity?
A. Coulomb/Meter square
B. Coulomb/Joule
C. Newton/Coulomb
D. Faraday/ Coulomb
Correct Answer: C
Solved Example: 9418-04
In a homogeneous electric field of magnitude 3 $\times$ 10$^4$ N, an electron is accelerated from rest. Determine its acceleration. (Ignore gravitation.) (mass of electron = 9.11 $\times$ 10$^{-31}$ kg)
A. 2.715 $\times$ 10$^{15}$ m/s$^2$
B. 5.265 $\times$ 10$^{15}$ m/s$^2$
C. 9.912 $\times$ 10$^{15}$ m/s$^2$
D. 4.441 $\times$ 10$^{15}$ m/s$^2$
\begin{align*} F&=qE\\ &=\left( 1.6\times 10^{-19}\right) \left( 3\times 10^{-4}\right) \\ &=5\times 10^{-15}N \end{align*} \begin{align*} a &=\dfrac{F}{m}\\ &=\dfrac{5\times 10^{-15}}{9.11\times 10^{-31}}\\ &=5.269\times 10^{15}m/s^{2} \end{align*}
Correct Answer: B
Solved Example: 9418-05
Infinite charges of magnitude q each are lying at x =1, 2, 4, 8... meter on X-axis. The value of the intensity of the electric field at point x = 0 due to these charges will be:
A. 12 $\times$ 10$^9$q N/C
B. Zero
C. 6 $\times$ 10$^9$q N/C
D. 4 $\times$ 10$^9$q N/C
\begin{align*} E &= \dfrac{q}{4 \pi \epsilon_0} \left(\dfrac{1}{1^2} + \dfrac{1}{2^2} + \dfrac{1}{4^2} + .... \right)\\ &= \dfrac{q}{4 \pi \epsilon_0} \left(\dfrac{1}{1} + \dfrac{1}{4} + \dfrac{1}{16} + .... \right)\\ &= \dfrac{q}{4 \pi \epsilon_0} \left(\dfrac{1}{1 - \dfrac{1}{4}} \right)\\ &=12 \times 10^9 q\ N/C \end{align*}
Correct Answer: A
Solved Example: 9418-05
If the electric field intensity is given by: \[\bar{E} = (x\bar{i}+ y\bar{j}+ z\bar{k})\ \mathrm{V/m},\] the potential difference between X(2, 0, 0) and Y(1, 2, 3) is:
A. +1 V
B. -1 V
C. +5 V
D. +6 V
\begin{align*} \bar{E} &= (x\bar{i}+ y\bar{j}+ z\bar{k})\\ \bar{dl} &= (dx\bar{i}+ dy\bar{j}+ dz\bar{k})\\ \bar{E} \cdot \bar{dl} &= xdx + ydy + zdz\\ \int \bar{E} \cdot \bar{dl} &= \int_1^2 (xdx) + \int_2^0 ydy + \int_3^0 zdz\\ \int \bar{E} \cdot \bar{dl} &= \dfrac{1}{2}\left[\left[x^2\right]_1^2 + \left[y^2\right]_2^0 + \left[z^2\right]_3^0\right]\\ \int \bar{E} \cdot \bar{dl} &= \dfrac{1}{2}\left[{3} + (-4) + (-9)\right]\\ \int \bar{E} \cdot \bar{dl} &= -5 \end{align*} \[ V = - \bar{E} \cdot \bar{dl} = -(-5) = 5\ \mathrm{V}\]
Correct Answer: C
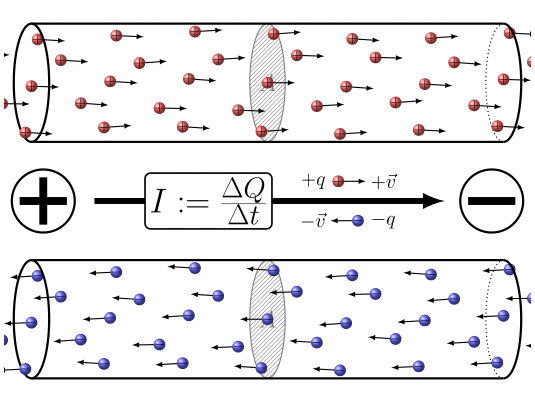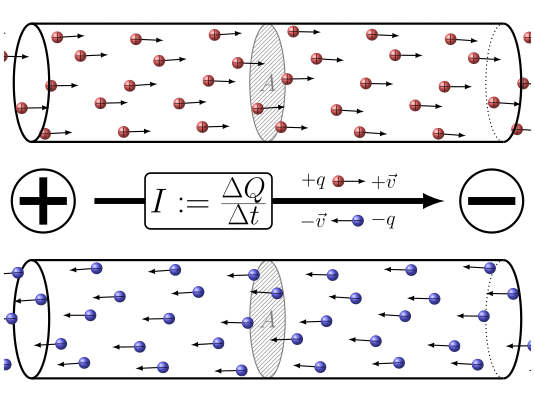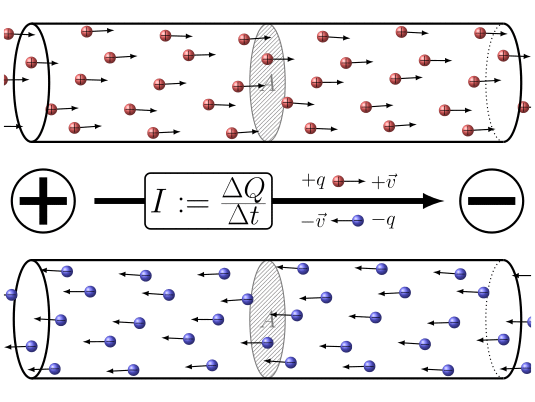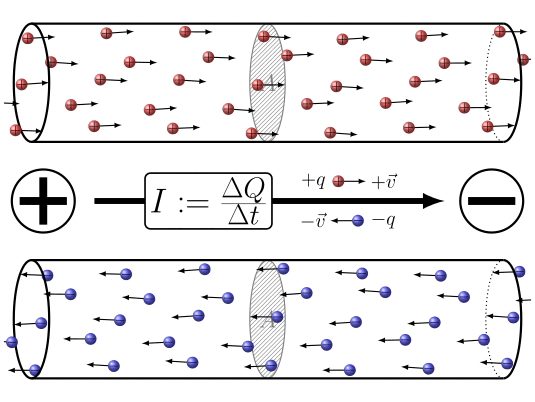
Electric Current
Learning Objectives:
- Define electric current.
- Calculate electric current from charge and time.
Electric current is defined as the rate at which charge flows through a surface (such as cross section of a wire).
Or in stedy state format, \[I = \dfrac{Q}{t}\] I = electric current rate at which charge flows in a certain pathway
Q = amount of charge flowing past a certain point
t = time
SI unit for electric current:
1 Ampere = 1 Coulomb/1 second
Solved Example: 18-3-01
Rate of flow of charge through cross-sectional area is known as:
A. Current
B. Voltage
C. Electric potential
D. Charge velocity
Correct Answer: A
Solved Example: 18-3-02
Current flowing through a conductor, when 2 $\times$ 10$^7$ electrons pass in 1 $\mu$sec will be:
A. 1.6 $\times$ 10$^{-6}$
B. 3.2 $\times$ 10$^{-6}$
C. 4.2 $\times$ 10$^{-6}$
D. 6 $\times$ 10$^{-6}$
Each electron has a charge of 1.6 $\times$ 10$^{-19}$ C.
\begin{align*}
\mathrm{current} = \dfrac{\mathrm{charge}}{\mathrm{time}}
&= \dfrac{1.6 \times 10^{-19} \times 2 \times 10^7}{1 \times 10^{-6}}\\
&= 3.2 \times 10^{-6}\ \mathrm{A}
\end{align*}
Correct Answer: B
Solved Example: 18-3-03
If the current flowing through a circuit is 0.6 A for 6 mins, the amount of electric charge flowing through it is:
A. 360 C
B. 216 C
C. 60 C
D. 36 C
\[i = \dfrac{q}{t}\] \[0.6 = \dfrac{q}{360}\] \[q = 216\ C\]
Correct Answer: C
Solved Example: 18-3-04
n identical cells each of e.m.f. E and internal resistance r are connected in series. An external resistance R is connected in series to this combination. The current through R is:
A. $\dfrac{nE}{R+nr}$
B. $\dfrac{nE}{nR+r}$
C. $\dfrac{E}{R+nr}$
D. $\dfrac{nE}{R+r}$
Correct Answer: A
Solved Example: 18-3-05
If 100 coulomb of charge passes through a conductor in 25 s, the current in the conductor is:
A. 1 A
B. 4 A
C. 10 A
D. 2.5 A
\begin{align*} i &= \dfrac{q}{t}\\ &= \dfrac{100}{25}\\ &= 4\ \mathrm{A} \end{align*}
Correct Answer: B
Solved Example: 18-3-06
Fill in the blank with the most appropriate option.
18 volts = _________ $\times$ 3 ohms.
A. 6 watts
B. 6 amperes
C. 6 milliamperes
D. 6 joules
\begin{align*} V &= IR\\ \dfrac{V}{R} &= I\\ \dfrac{18\ \mathrm{Volts}}{3\ \mathrm{\Omega}} &= 6\ \mathrm{Ampere} \end{align*}
Correct Answer: B
Resistance
Learning Objectives:
- Define resistance (R) and know how it can be altered.
- Use Ohm’s law to design circuits.
- Calculate resistance from resistivity (conductivity).
Electrical Resistance:
Electrical resistance is a measure of the difficulty to pass an electric current through that conductor. \[R = \dfrac{V}{I}\] or more commonly written as:
An object or device with greater resistance will require a greater voltage to produce a certain amount of current.
SI unit for resistance is Ohm:
1 Ohm = 1 Volt/1 Ampere or W = \(\dfrac{V}{A}\)
(The number of ohms indicates how many volts are required to produce 1 Ampere of current.)

The original uploader was Chggr at Greek Wikipedia., CC BY-SA 3.0, via Wikimedia Commons

Gorkaazk, CC0, via Wikimedia Commons
Resistance in Series:
Components connected in series are only connected to each other at one point.
The same current flows through both components. The sum of the voltages across each component in the circuit equals the power supply voltage.
Resistance in Parallel:
The components sit side by side and connect to more than one other component.
The voltage is the same across all parallel components.
The sum of the currents in each branch of the circuit equals the current leaving the power supply.
Omegatron, CC BY-SA 3.0, via Wikimedia Commons
Resistivity:
Resistivity is a measure of the resisting power of a specified material to the flow of an electric current.
For a conductor of length L, electrical resistivity \(\rho\), and cross-sectional area A, the resistance is:
Internal Resistance:
Internal resistance is the resistance within a battery, or other voltage source, that causes a drop in the source voltage when there is a current. Thus, the voltage \(V\) of the battery is related to its emf \(E\) and internal resistance \(r\) via \[V = {E} - I\,r.\]
MikeRun, CC BY-SA 4.0, via Wikimedia Commons
Effect of Temperature on Resistance and Resistivity:
where,
$\alpha$ = Temperature coefficient
Solved Example: 18-4-01
Internal resistance of cell when there is current of 0.40 A when a battery of 6.0 V is connected to a resistor of 13.5 $\Omega$ is:
A. 1.5 $\Omega$
B. 2.3 $\Omega$
C. 3.5 $\Omega$
D. 4.5 $\Omega$
Total resistance of the circuit, including internal resistance, can be calculated by:
\[R = \dfrac{V}{I}
= \dfrac{6}{0.4}
= 15\ \Omega\]
This resistance is including internal resistance. Out of this 15 $\Omega$ , 13.5 $\Omega$ is external resistance.
Internal resistance,
\[ r = R_{Total} - R_{External} = 15 - 13.5 = 1.5\ \Omega\]
Correct Answer: A
Solved Example: 18-4-02
Maximum current a battery of e.m.f. 3.0 V and internal resistance 1.0 $\Omega$ is:
A. 4.0 A
B. 5.0 A
C. 3.0 A
D. 30 A
Maximum current will flow, when the ends of the battery are short-circuited, i.e. the external resistance will be zero.
In such case, the electrons will encounter only internal resistance of the battery.
\[i = \dfrac{V}{R}
= \dfrac{3}{1}
= 3\ A\]
Correct Answer: C
Solved Example: 18-4-03
The resistance of an electric bulb drawing 1.2 A current at 6.0 V is ______________.
A. 0.5 $\Omega$
B. 5 $\Omega$
C. 0.2 $\Omega$
D. 2 $\Omega$
\[R = \dfrac{V}{I} = \dfrac{6}{1.2} = 5\ \Omega\]
Correct Answer: B
Solved Example: 18-4-04
The unit of resistivity is _________________.
A. Ohm
B. Ohm / m
C. Ohm-m
D. Mho
Correct Answer: C
Solved Example: 18-4-05
Specific resistance of a wire can be measured by formula:
A. $\dfrac{R}{L}$
B. $\dfrac{RA}{L}$
C. $\dfrac{RL}{A}$
D. $\dfrac{A}{RL}$
Resistance of a wire depends as follows:
Directly proportional to the length of the wire,
Inversely proportional to the cross-sectional area of the wire
\[R \propto \dfrac{L}{A} = \rho \cdot \dfrac{L}{A}\] Hence, \[\rho = \dfrac {RA}{L}\]
Correct Answer: B
Solved Example: 18-4-06
Current of 0.75 A, when a battery of 1.5 V is connected to wire of 5 m having cross sectional area 2.5 $\times$ 10$^{-7}$ m$^2$, will have resistivity, in $\Omega$.m:
A. 1 $\times$ 10$^{-7}$
B. 1.1 $\times$ 10$^{-7}$
C. 2 $\times$ 10$^{-7}$
D. 2.1 $\times$ 10$^{-7}$
\[R = \dfrac{V}{I} = \dfrac{1.5}{0.75} = 2\ \Omega\] Also, \begin{align*} R &= \dfrac{\rho \cdot L }{ A}\\ 2 &= \dfrac{\rho \cdot 5}{2.5 \times 10^{-7}}\\ \rho &= \dfrac{2 \times 2.5 \times 10^{-7}}{5} = 1 \times 10^{-7}\ \Omega.m \end{align*}
Correct Answer: A
Solved Example: 18-4-07
Resistivity of a wire depends on:
A. Length
B. Material
C. Cross section area
D. None of the above
textbfResistance of a wire depends upon three factors.
The length of the wire,
The cross-sectional area of the wire, and
The resistivity of the material composing the wire.
Resistivity should not be confused with
resistance of a wire.
Resistivity is a specific property of a material. It depends only upon
the material, and NOT on other geometrical factors such as
length or cross-sectional area.
Correct Answer: B
Solved Example: 19-4-08
The potential difference across a cell in an open circuit is 8 V. It falls to 4 V when a current of 4 A is drawn from it. The internal resistance of the cell is :
A. 4 $\Omega$
B. 3 $\Omega$
C. 2 $\Omega$
D. 1 $\Omega$
\begin{align*} V &= E - ir \\ 4 &= 8 - 4(r)\\ 4r &= 4 \\ r &= 1\ \Omega \end{align*}
Correct Answer: D
Solved Example: 19-4-09
The effective resistance of a parallel connection that consists of four wires of equal length, equal area of cross-section and same material is 0.25 $\Omega$. What will be the effective resistance if they are connected in series?
A. 0.25 $\Omega$
B. 0.5 $\Omega$
C. 1 $\Omega$
D. 4 $\Omega$
When 'n' equal resistances of a value R each are connected in parallel, their effective resistance becomes $\left(\dfrac{R}{n}\right)$. \[\dfrac{R}{4} = 0.25\] \[R = 1\ \Omega\] When 'n' equal resistances of a value R each are connected in series, their effective resistance becomes $nR$. \[nR = 4 \times 1 = 4\ \Omega\]
Correct Answer: D
Electric Power
Learning Objectives:
- Define the concept of power and understand the relationship between current, voltage, and power.
- Calculate power in electric circuits.
- Understand heating effect of electric current.
Electric power is the rate, per unit time, at which electrical energy is transferred by an electric circuit.
The SI unit of power is the Watt, one Joule per Second.
Solved Example: 18-5-01
If we double both current and voltage keeping resistance constant then power is:
A. Unchanged
B. Halves
C. Doubles
D. Quadruples
\[P = V_{new} \cdot I_{new} = 2V_{old} \cdot 2I_{old} = 4P_{old}\]
Correct Answer: D
Solved Example: 18-5-02
If a light bulb is switched on for 40 s and it consumes 2400 J of electrical energy then its power is:
A. 60 W
B. 70 W
C. 80 W
D. 90 W
$P = \dfrac{W}{t} = \dfrac{2400}{40} = 60\ W$
Correct Answer: A
Solved Example: 18-5-03
Amount of energy supplied by current in unit time is called:
A. Electric energy
B. Electric power
C. Resistance
D. Friction
Rate of energy is power. If the power is given by displacement of body, it is mechanical power. If it is given by movement of electrons (in the form of current), it is electrical power.
Correct Answer: B
Solved Example: 18-5-04
If resistance of an electric bulb is 500 $\Omega$ and voltage across its ends is 250 V then power consumed by it is:
A. 130 W
B. 125 W
C. 120 W
D. 200 W
$P = V \cdot I = V \cdot \left(\dfrac{V}{R}\right) = \dfrac{V^2}{R} = \dfrac{250^2}{500} = 125\ W$
Correct Answer: B
Solved Example: 18-5-05
If 12 V are applied to a circuit that consumes 78 Watt, what is the current flow through circuit?
A. 6.5 A
B. 0.65 A
C. 65 mA
D. 12 A
\begin{align*} P &= V I \\ 78 &= (12) I \\ I &= 6.5\ \mathrm{A} \end{align*}
Correct Answer: A
Solved Example: 18-5-06
An electric bulb rated 200 V and 100 W is connected to a 160 V power supply. What power will be consumed by the bulb?
A. 64 W
B. 80 W
C. 100 W
D. 160 W
Correct Answer: A
Solved Example: 18-5-07
If current = 1.414 A and resistance = 50$\Omega$, then find power.
A. 400 Watts
B. 100 Watts
C. 300 Watts
D. 200 Watts
\begin{align*} P &= i^2R\\ &= (1.414)^2\ times 50\\ &= 100\ \mathrm{W} \end{align*}
Correct Answer: B
Magnetostatics
Learning Objectives:
- Define the concept of magnetism.
- Be able to calculate electromagnetic forces and fields.
Magnetic Flux ($\phi$):
The magnetic flux is defined as the total number of magnetic lines of force in a magnetic field. It is denoted by ‘\(\phi\)’ and is measured in Webber (Wb). One Webber is defined as the flux radiated out by a unit N-pole.
1Wb = 10\(^8\) lines of force
Magnetic Flux Density (B):
The flux per unit area (A), measured in a plane perpendicular to the flux is defined as the flux density. It is measured in tesla (T) or (Wb/m\(^2\)).
\[B = \dfrac{\phi}{A}\]
Magnetic Field Strength or Magnetic Field Intensity (H):
The magnetic field strength at a point in the magnetic field is defined as the force experienced by a unit North Pole placed at that point in the magnetic field. It is measured in Newton per Weber (N/Wb).
Energy stored in Magnetic Field:
Geek3, CC BY-SA 3.0, via Wikimedia Commons
File:Flusso magnetico attraverso una superficie perpendicolare.svg: User:ARTEderivative work: MikeRun, Public domain, via Wikimedia Commons
Solved Example: 18-6-01
Which, among the following qualities, is not affected by the magnetic field?
A. Moving charge
B. Change in magnetic flux
C. Current flowing in a conductor
D. Stationary charge
A stationary charge is not affected by a magnetic field because stationary charges do not have any velocity. Magnetic field cannot occur in a particle having zero velocity.
Correct Answer: D
Solved Example: 18-6-02
Magnetomotive force is equal to:
A. Current / number of turns per unit length
B. Current * number of turns per unit length
C. Current * number of turns
D. Current / number of turns
MMF is ability to produce flux = product of current flowing and number of turns.
Correct Answer: C
Solved Example: 18-6-03
The relation between the direction of current and the direction of magnetic field is?
A. Same direction
B. Opposite direction
C. Perpendicular
D. Unrelated
When a conductor carries current, the force developed in the conductor, the current in the conductor and the magnetic field in the conductor are mutually perpendicular to each other.
Correct Answer: C
Solved Example: 18-6-04
Calculate the magnetic flux density, in T, if the magnetic field strength is 2 A/m.
A. $4 \pi \times 10^{-7}$
B. $8 \pi \times 10^{-7}$
C. $10 \pi \times 10^{-7}$
D. $12 \pi \times 10^{-7}$
We know that:
$\mu_0=\dfrac{B}{H}$.
Substituting H from the question, we get B = $8 \pi \times 10^{-7}$ T.
Correct Answer: B
Solved Example: 18-6-05
Calculate the magnetic field strength if the magnetic flux density is 4 $\times \pi \times$ T.
A. $10^{-7}/16*\pi^2$A/m
B. $10^{-7}$A/m
C. $10^7$A/m
D. $10^{-7}$A
We know that:
$\mu_0=\dfrac{B}{H}$.
H = $10^7$ A/m.
Correct Answer: C
Solved Example: 18-6-06
Find H = ___________ A/m at the center of a circular coil of diameter 1 m and carrying a current of 2 A.
A. 0.6366
B. 0.1636
C. 6.366
D. 2
The magnetic field intensity of a cirular coil is given by: \begin{align*} H &=\dfrac{I}{2R}\\ &=\dfrac{2}{2\times 0.5}\\ &=2\ \mathrm{A/m} \end{align*}
Correct Answer: D
Solved Example: 18-6-07
Calculate the flux density at a distance of 5 cm from a long straight circular conductor carrying a current of 250 A and placed in air.
A. 10$^2$ Wb/m$^2$
B. 10$^{-2}$ Wb/m$^2$
C. 10$^{-3}$ Wb/m$^2$
D. 10$^3$ Wb/m$^2$
\begin{align*} B &=\mu_0 \cdot H\\ &=\mu _{0}\dfrac{I}{2\pi r}\\ &=4\pi \times 10^{-7}\times \dfrac{250}{2\pi \times 5\times 10^{-2}}\\ &=10^{-3}\ \mathrm{Wb/m}^{2} \end{align*}
Correct Answer: C
Solved Example: 18-6-08
Two identical coils A and B of 1000 turns each lie in parallel plane such that 80% of the flux produced by one coil links with the other. If a current of 5 A flowing in A produces a flux of 0.05 mWb, then the flux linking with coil B is:
A. 0.4 mWb
B. 0.04 mWb
C. 4 mWb
D. 0.004 mWb
Correct Answer: B
Solved Example: 18-6-09
The S.I. unit magnetic permeance is:
A. Henry
B. Weber
C. Tesla
D. Coulomb
Correct Answer: A
Solved Example: 18-6-10
Magnetic flux will be _________ if the surface area vector of a surface is perpendicular to the magnetic field.
A. Zero
B. Unity
C. Close to maximum
D. Maximum
Correct Answer: A
Solved Example: 18-6-11
A coil of 360 turns is linked by a flux of 200 $\mu$ Wb. If the flux is reversed in 0.01 second, then find the EMF induced in the coil.
A. 7.2 V
B. 0.72 V
C. 14.4 V
D. 144 V
Since the flux is reversed, the change in flux is from +200 $\mu$ Wb to -200 $\mu$ Wb = 400 $\mu$ Wb. \begin{align*} E &= N \dfrac{d\phi}{dt}\\ &= 360 \times \dfrac{400 \times 10^{-6}}{0.01}\\ &= 14.4\ V \end{align*}
Correct Answer: C
Solved Example: 18-6-12
Two magnetic poles are located 5 cm apart in air. If each pole has a strength of 5 mWb, find the force of repulsion between them.
A. $\dfrac{1}{{{\pi ^2}}}N$
B. $\dfrac{6250}{{{\pi ^2}}}N$
C. $\dfrac{625}{{{\pi ^2}}}N$
D. $\dfrac{62.5}{{{\pi ^2}}}N$
Correct Answer: B
Solved Example: 18-6-13
A long straight circular conductor placed in air is carrying a current of 250 A. Find the magnetising force at a distance of 5 cm from the conductor.
A. $\dfrac{{5000}}{\pi }AT/m$
B. $\dfrac{{500}}{\pi }AT/m$
C. $2500 AT/m$
D. $\dfrac{{2500}}{\pi }AT/m$
Correct Answer: D
Solved Example: 18-6-14
The force on the current-carrying conductor in a magnetic field depends upon:
(a) the flux density of the field
(b) The strength of the current
(c) The length of the conductor perpendicular to the magnetic field
(d) The directions of the field and the current
A. (a), (c) and (d) only
B. (a), (b)and (c) only
C. (a), (b) and (d) only
D. (a), (b), (c) and (d)
Correct Answer: D
Voltage
Learning Objectives:
- Understand the meaning and significance of electric potential.
- Use integration to determine electric potential difference between two points on a line.
- Calculate how much work is required to move a test charge from one location to another in the field of fixed point charges.
Solved Example: 18-2-01
Energy stored in a condenser of capacity 10 $\mu F$, charged to 6 kV is used to lift a mass of 10g. The height to which the body can be raised is:
A. 180 m
B. 18 m
C. 1.8 m
D. 1800 m
Energy stored in a condenser \begin{align*} E &= \dfrac{1}{2} CV^2 \\ &= \dfrac{1}{2} \times 10 \times 10^{-6} \times 6000^2 \\ &= 180\ J \end{align*} This will be equal to the potential energy. \begin{align*} 180 &= mgh \\ 180 &= 0.010 \times 9.81 \times h \\ h &= 1834\ m \end{align*}
Correct Answer: D
Solved Example: 18-2-04
In an experiment, a charged drop of oil of mass 1.8 $\times 10^{-14}$ kg is stationary between the plates of a parallel plate condenser separated by a distance of 9 mm and charged to a potential difference of 2000 V. The charge on the drop is:
A. 8 $\times 10^{-19}$ C
B. 6 $\times 10^{-19}$ C
C. 5 $\times 10^{-19}$ C
D. 4 $\times 10^{-19}$ C
Vertical Force = qE
But
\[E = \dfrac{V}{d}
= \dfrac{2 \times 10^3}{9 \times 10^{-3}}
= 0.22 \times 10^6 V/m\]
Also, qE = mg
\[q = \dfrac{mg}{E}
=\dfrac{1.8 \times 10^{-14} \times 9.8}{0.22 \times 10^6}
=8.02 \times 10^{-19} C\]
Correct Answer: A
Solved Example: 18-2-05
Point charge q moves from point P to point S along the path PQRS (figure shown) in a uniform electric field E pointing coparallel to the positive direction of the X-axis. The coordinates of the points P,Q,R and S are (a,b), (2a,0), (a,-b) and (0,0) respectively. The work done by the field in the above:
A. qEa
B. qE$\sqrt{(2a)^2+b^2}$
C. qEa$\sqrt{2}$
D. -qEa
As electric field is a conservative field Hence the work done does not depend on path. Instead of following red path, we can follow blue path as shown in the figure, which is much simpler.
\begin{align*} W_{PQRS} &= W_{POS} = W_{PO} + W_{OS}\\ &=Fb \cos 90^\circ +Fa \cos180^\circ\\ &=0 + qEa(1)\\ &=qEa \end{align*}Correct Answer: A
Solved Example: 18-2-06
A capacitor is charged by using a battery which is then disconnected. A dielectric slab is then slipped between the plates, which results in:
A. Reduction of charge on the plates and increase of potential difference across the plates.
B. Increase in the potential difference across the plate, reduction in stored energy, but no change in the charge on the plates.
C. Decrease in the potential difference across the plates, reduction in the stored energy, but no change in the charge on the plates.
D. None of the above.
Battery in disconnected so Q will be constant as C $\propto$ K. So with introduction of dielectric slab capacitance will increase using Q = CV, V will decrease and using U= $\dfrac{Q^2}{2C}$, energy will decrease.
Correct Answer: C
Solved Example: 18-2-07
How much work has to be done to transfer a charge of 3C across two points having a potential difference of 10V?
A. -30 A
B. 30 A
C. -30 J
D. 30 J
\begin{align*} V_{1-2} &= \dfrac{W_{1-2}}{q}\\ W_{1-2} &= V_{1-2} \times q\\ &= 10 \times 3\\ &= 30\ \mathrm{J} \end{align*}
Correct Answer: D
Solved Example: 18-2-08
A practical voltage source can also be represented as:
A. A resistance in series with an ideal current source
B. A resistance in series with an ideal voltage source
C. A resistance in parallel with an ideal voltage source
D. None of the mentioned
Correct Answer: B
Solved Example: 18-2-09
A battery of EMF 6.0 V and internal resistance 1.0 $\Omega$ is connected to a resistor of 11 $\Omega$. The terminal potential difference for the battery is:
A. 6.0 V
B. 5.5 V
C. 5.2 V
D. 4.5 V
\begin{align*} i &= \dfrac{E}{R + r}\\ &= \dfrac{6}{11 + 1}\\ &= 0.5\ \mathrm{A} \end{align*} \begin{align*} V &= E - ir\\ &= 6 - (0.5)(1) = 5.5\ \mathrm{V} \end{align*}
Correct Answer: B
Solved Example: 18-2-10
A battery with an internal resistance of 2 $\Omega$ and an emf of 4.0 V is connected in series to a load resistance and the terminal voltage falls to 3.8 V. What current is flowing in the circuit, and what is the value of the load resistance?
A. 0.01 A, 280 $\Omega$
B. 0.1 A, 38 $\Omega$
C. 0.01 A, 380$\Omega$
D. 0.1 A, 28$\Omega$
\begin{align*} V &= E - iR\\ 3.8 &= 4 - i(2)\\ i &= 0.1\ \mathrm{A} \end{align*} \begin{align*} E &= i(R + r)\\ R + r &= \dfrac{E}{i}\\ R + 2 &= \dfrac{4}{0.1}\\ R &= 40 - 2 = 38\ \Omega \end{align*}
Correct Answer: B
Solved Example: 3454
What is the unit of electric potential?
A. Ampere
B. Volt
C. Ohm
D. Coulomb
Correct Answer: B
Solved Example: 435345
Voltage is defined as:
A. The flow of electric charge
B. The energy per unit charge
C. The resistance to current flow
D. The total charge in a circuit
Correct Answer: B
Solved Example: 565464
Voltage is defined as:
A. The flow of electric charge
B. The energy per unit charge
C. The resistance to current flow
D. The total charge in a circuit
Correct Answer: B
Solved Example: 56768
Which of the following circuits has the highest voltage?
A. Series circuit with three 1.5V batteries
B. Parallel circuit with two 9V batteries
C. Series circuit with two 9V batteries
D. Parallel circuit with three 1.5V batteries
Correct Answer: C
Induced Voltage
Learning Objectives:
- Knowing the magnetic field's strength, the surface area, and the angle between the surface's normal and the magnetic field, calculate the magnetic flux across a surface.
- Calculate the size of the induced emf in a closed loop as a result of changing magnetic flux through the loop using Faraday's law.
Faraday's Law:
Solved Example: 9510-01
Choose the expression for Faraday's second Law of Electromagnetic Induction.
Note: $\epsilon$ is the electromotive force,$\phi$ is the magnetic flux, N is the number of turns
A. $\epsilon \ = -Nd \ \phi /dt$
B. $\epsilon = Nd \ \phi /dt$
C. $\epsilon = N2d \ \phi /dt$
D. $\epsilon = -N(d \ \phi /dt)^2$
Correct Answer: B
Solved Example: 9510-02
A flux of 0.25 mWb is produced by a coil of 1000 turns wound on a ring with a current of 2 A in it. Calculate the e.m.f. induced in the coil when a current of 10 A is switched off, assuming the current will fall to zero in 1 millisecond.
A. 2500 V
B. 25 V
C. 1250 V
D. 12.5 V
The inductance of a coil is given by: \begin{align*} L &= \dfrac{N\phi}{I}\\ &= \dfrac{1000 \times 0.25 \times 10^{-3}}{2}\\ &= 0.125\ H \end{align*} EMF induced \begin{align*} E &= L \dfrac{d\phi}{dt}\\ &= 0.125 \dfrac{(10-0)}{1 \times 10^{-3}}\\ &= 1250\ V \end{align*}
Correct Answer: C