Conduction
Fourier's Law of Heat Conduction
Learning Objectives:
- Understand and are able to recognize conduction, convection and radiation as modes of heat transfer.
- Fourier’s law of conduction.
- Able to solve one-dimensional heat conduction problems using the energy equation and Fourier’s law.
Conduction expressed by Fourier’s law of heat conduction as written below:
Where, \(\displaystyle \dfrac{dT}{dx}\) is the temperature gradient. k is the thermal conductivity A is the area which is normal to the direction of heat transfer.
Cdang, CC BY-SA 3.0, via Wikimedia Commons
Solved Example: 80-1-01
Fourier's law of heat conduction is valid for:
A. One dimensional cases only
B. Two dimensional cases only
C. Three dimensional cases only
D. Regular surfaces having non-uniform temperature gradients
Among the assumptions for Fourier's law of heat conduction, the main ones are: Steady state heat conduction, one directional heat flow and no internal heat generation. For two dimensional steady state heat conduction, Laplace equation is used.
Correct Answer: A
Solved Example: 80-1-02
Unit of thermal conductivity in S.I. units is:
A. J/m$^2$ sec
B. J/m $^\circ$K sec
C. W/m $^\circ$K
D. (B) and (C) above.
In the International System of Units (SI), thermal conductivity is measured in Watts per meter-Kelvin (W/(m$\cdot$K)). Note that Watt is Joule/second.
In Imperial units, thermal conductivity is measured in BTU/(h $\cdot$ ft $\cdot$ $^\circ$F).
Correct Answer: D
Solved Example: 80-1-03
Thermal conductivity of non-metallic amorphous solids with decrease in temperature:
A. Increases
B. Decreases
C. Remains constant
D. May increase or decrease depending on temperature
Correct Answer: B
Solved Example: 80-1-04
The insulation ability of an insulator with the presence of moisture would:
A. Increases
B. Decrease
C. Remain unaffected
D. May increase/decrease depending on temperature and thickness of insulation
Correct Answer: B
Solved Example: 80-1-06
Pick up the wrong case.
Heat flowing from one side to other depends directly on:
A. Face area
B. Time
C. Thickness
D. Temperature difference
Refer Fourier's law of heat conduction: \[Q = - K A \dfrac{dT}{dx}\]
Heat transfer due to conduction depends directly on Area as well as temperature difference as both terms are in the numerator. Also, this formula gives you heat transfer per unit time. Hence, total heat transfer also depends directly on time. However, heat transfer by conduction depends inversely on thickness.
Correct Answer: C
Solved Example: 80-1-07
Metals are good conductors of heat because:
A. Their atoms collide frequently
B. Their atoms are relatively far apart
C. They contain free electrons
D. They have high density
Metals have free electrons in their outermost shells, which are responsible for good conduction of heat as well as electricity.
Correct Answer: C
Solved Example: 80-1-08
Which of the following is a case of steady state heat transfer:
A. I.C. engine
B. Air preheaters
C. Heating of building in winter
D. None of the above.
Correct Answer: D
Solved Example: 80-1-09
Heat flows from one body to other when they have:
A. Different heat contents
B. Different specific heat
C. Different atomic structure
D. Different temperatures
Heat flow takes places when the temperatures of two bodies are different. This is true even when the body with lower temperature has higher heat content. Heat flow is analogous to fluid flow, where fluid flows from higher level to lower level, even though the lower level reservoir has more fluid content. The 'level' in fluid flow is similar to 'temperature' in heat flow.
Correct Answer: D
Solved Example: 80-1-10
In heat transfer, conductance equals conductivity (kcal/hr/sqm/$^\circ$C/cm) divided by:
A. hr (time)
B. sq m (area)
C. $^\circ$C (temperature)
D. cm (thickness)
Conductance is inverse of thermal resistance. \[U = \dfrac{1}{R}\] It can be calculated as: \[U = \dfrac{k}{L}\]
Correct Answer: D
Solved Example: 80-1-11
The amount of heat flow through a body by conduction is:
A. Directly proportional to the surface area of the body
B. Directly proportional to the temperature difference on the two faces of the body
C. Inversely proportional to the thickness of the body
D. All of the above.
By Fourier's law of Heat Conduction, \[Q = - kA\dfrac{dT}{dx}\] Hence, Heat transfer by conduction is:
- Directly proportional to the surface area of the body
- Directly proportional to the temperature difference on the two faces of the body
- Inversely proportional to the thickness of the body
Correct Answer: D
Solved Example: 80-1-13
Which of the following is expected to have highest thermal conductivity?
A. Steam
B. Solid ice
C. Melting ice
D. Water
Correct Answer: B
Solved Example: 80-1-15
Which of the following has maximum value of thermal conductivity?
A. Aluminum
B. Steel
C. Brass
D. Copper
Correct Answer: A
Solved Example: 80-1-16
Moisture would find its way into insulation by vapour pressure unless it is prevented by:
A. High thickness of insulation
B. High vapour pressure
C. Less thermal conductivity insulator
D. A vapour seal
Correct Answer: D
Solved Example: 80-1-17
Thermal diffusivity is:
A. A dimensionless parameter
B. Function of temperature
C. Used as mathematical model
D. A physical property of the material
Thermal diffusivity can be calculated as: \[\alpha = \dfrac{k}{\rho c}\] It is a physical property of a material, indicating how quickly or 'swiftly' heat can pass through the material.
Correct Answer: D
Solved Example: 80-1-19
Unit of thermal diffusivity is:
A. m$^2$/s
B. m$^2$/s$^\circ$C
C. kcal/m$^2$ s
D. kcal/m.s$^\circ$C
Thermal diffusivity can be calculated as: \[\alpha = \dfrac{k}{\rho c}\] \[k = W/m.k = \dfrac{\dfrac{J}{s}}{m.k}\] \[\rho = kg/m^3\] \[c = J/kg.K\] \[\alpha = \dfrac{\dfrac{\dfrac{J}{s}}{m.k}}{kg/m^3 J/kg.K} = m^2/s\]
Correct Answer: A
Solved Example: 80-1-21
Heat conducted through unit area and unit thick face per unit time when temperature difference between opposite faces is unity, is called:
A. Thermal resistance
B. Thermal coefficient
C. Temperature gradient
D. Thermal conductivity
Correct Answer: D
Solved Example: 80-1-22
Which of the following property of air does not increase with rise in temperature:
A. Thermal conductivity
B. Thermal diffusivity
C. Density
D. Dynamic viscosity
Correct Answer: C
Solved Example: 80-1-23
The thermal diffusivities for gases are generally:
A. More than those for liquids
B. Less than those for liquids
C. More than those for solids
D. Dependent on the viscosity
Correct Answer: A
Solved Example: 80-1-24
The thermal diffusivities for solids are generally:
A. Less than those for gases
B. Less than those for liquids
C. More than those for liquids and gases
D. More or less same as for liquids and gases
Correct Answer: C
Solved Example: 80-1-26
Which one of the following states the fundamental modes of heat transfer?
A. Friction, Convection, Nuclear reactions.
B. Conduction, Convection, Radiation
C. Ionization, Evaporation, Radiation
D. Chemical reaction, Electrical resistance, Nuclear reactions.
Correct Answer: B
Thermal Resistance of Various Objects
Learning Objectives:
- Explain the concept of thermal conductivity and thermal resistance.
- Explain the similarities and relationship of thermal and electrical conductivity.
- Compute thermal resistance for individual items such as plane wall, pipes and spheres with or without insulation.
- Describe the concept of thermal resistance of air layers.
- Identify series and parallel combinations from real-life thermal insulation scenarios for application of thermal resistance concepts.
- Evaluate thermal resistance of simple shapes such as plane wall, cylindrical wall.
- Evaluate thermal resistance of thin air film layer.
There is an electrical analogy with conduction heat transfer that can be exploited in problem solving. Just as an electrical resistance is associated with the conduction of electricity, a thermal resistance may be associated with the conduction of heat.
The rate of heat transfer through a plane wall corresponds to the electric current, the thermal resistance corresponds to electrical resistance and the temperature difference corresponds to voltage difference across the plane wall.
Equivalent thermal circuits may be used for more complex systems, such as composite walls. Such walls may involve any number of series and parallel thermal resistances due to layers of different materials.
The thermal resistance is defined as the ratio of the temperature difference, dT, to the heat transfer Q. This is analogous to Ohm’s law, in which the electrical resistance is defined as the ratio of the voltage drop across a resistor to the current flow across the resistor. Thermal resistance is a heat property and a measurement of a temperature difference by which an object or material resists a heat flow (heat per time unit or thermal resistance). Thermal resistance is the reciprocal of thermal conductance.
Defining resistance as the ratio of a driving potential to the corresponding transfer rate, it follows that the thermal resistance for conduction is: \[R = \dfrac{T_1 - T_2}{q_x} = \dfrac{L}{kA}\]
Ellande, CC BY-SA 4.0, via Wikimedia Commons
Plain Wall:
Cylindrical Wall:
Convection Resistance:
Solved Example: 80-2-01
A furnace is made of a red brick wall of thickness 0.5 m and conductivity 0.7 W/mK. For the same heat loss and temperature drop, this can be replaced by a layer of diatomite earth of conductivity 0.14 W/mK and thickness:
A. 0.5 m
B. 0.1 m
C. 0.2 m
D. 0.25 m
Here to achieve the same heat transfer and temperature drop, the conductive resistance should be kept same.
\[R= \dfrac{t}{k}\]
where t= thickness of wall and k= conductivity of material.
So,
\[R = \dfrac{0.5}{0.7}= \dfrac{t}{0.14}, \ \ t = 0.1\ m\]
This is thickness for wall of new material.
Correct Answer: B
Solved Example: 80-2-02
A furnace wall made of steel plate 10 mm thick and thermal conductivity 15 kcal/m-hr-°C is lined inside with silica brick of 150 mm thick of thermal conductivity 1.75 kcal/m-hr-°C and on outside with magnesia bricks of 200 mm thick with thermal conductivity of 4.5 kcal/m-hr-°C. The total resistance of the composite wall will be:
A. 0.13 $^\circ$C hr/kcal
B. 0.23 $^\circ$C hr/kcal
C. 0.03 $^\circ$C hr/kcal
D. 0.33 $^\circ$C hr/kcal
\begin{align*} R &= \dfrac{L_1}{K_1A} + \dfrac{L_2}{K_2A} + \dfrac{L_3}{K_3A}\\ &= \dfrac{0.2}{4.5} + \dfrac{0.010}{15} + \dfrac{0.150}{1.75}\\ &= 0.130\ ^\circ \mathrm{C.hr/kcal} \end{align*}
Correct Answer: A
Solved Example: 80-2-03
For steady state one-dimensional heat conduction through a plane wall with constant thermal conductivity and no internal heat generation, the temperature distribution within the wall will be:
A. Hyperbolic
B. Elliptic
C. Linear
D. Non-linear
Correct Answer: C
Solved Example: 80-2-04
A composite wall of surface area 1 m$^2$ has three layers of thickness 0.3 m, 0.2 m, and 0.1 m and has thermal conductivities 0.6, 0.4, and 0.1 W/m$^\circ$C, respectively. There is no generation of thermal energy within the wall. If the inner and outer temperatures of the composite wall are 1840$^\circ$C and 340$^\circ$C, respectively, the rate of heat transfer through this wall is:
A. 0.75 kW
B. 0.150 kW
C. 7.5 kW
D. 1.5 kW
\begin{align*} R &= \dfrac{L_1}{K_1A} + \dfrac{L_2}{K_2A} + \dfrac{L_3}{K_3A}\\ &= \dfrac{0.3}{0.6} + \dfrac{0.2}{0.4} + \dfrac{0.1}{0.1}\\ &= 2\ ^\circ \mathrm{C.hr/kcal} \end{align*} \begin{align*} \dot{Q} &= \dfrac{\Delta T}{R} \\ &=\dfrac{1840 - 340}{2} \\ &= \dfrac{1500}{2} \\ &= 750\ W \\ &= 0.750\ KW \end{align*}
Correct Answer: A
Solved Example: 80-3-01
In a hollow cylindrical tube of length L, conductivity k, inner radius r and outer radius $r_o$, if $T_i$ is greater than $T_o$, the thermal resistance is:
A. $\dfrac{1}{2\pi kL} ln \left ( \dfrac{r_i}{r_o} \right )$
B. $\dfrac{1}{2\pi kL} ln \left ( \dfrac{r_o}{r_i} \right )$
C. $\dfrac{1}{2\pi kL} ln \left ( r_i \times r_o \right )$
D. $2\pi kL ln \left ( \dfrac{r_i}{r_o} \right )$
Correct Answer: B
Solved Example: 80-3-02
A 160 mm diameter pipe carrying saturated steam is covered by layer of lagging of thickness of 40 mm (k=0.8 W/m $^{\circ}\mathrm{C}$) later, an extra layer of lagging 10 mm thick (k=1.2 W/m $^{\circ}\mathrm{C}$) is added. If the surrounding temperature remains constant and heat transfer coefficient for both the lagging materials is 10 W/sq m $^{\circ}\mathrm{C}$, determine the percentage change in the rate of heat loss due to extra lagging layer.
A. 0.193%
B. 0.113%
C. 0.223%
D. 0.563%
Correct Answer: C
Solved Example: 80-4-01
Consider one-dimensional steady state heat conduction along x-axis (0 < x < L), through a plane wall with the boundary surfaces (x=0 and x=L) maintained at temperatures of 0$^{\circ}\mathrm{C}$ and 100$^{\circ}\mathrm{C}$. Heat is generated uniformly throughout the wall. Choose the CORRECT statement.
A. The temperature distribution is symmetric about the mid-plane of the wall.
B. The direction of heat transfer will be from the surface at 100$^{\circ}\mathrm{C}$ to the surface at 0$^{\circ}\mathrm{C}$.
C. The temperature distribution is linear within the wall.
D. The maximum temperature inside the wall must be greater than 100$^{\circ}\mathrm{C}$.
Since heat is generated uniformly throughout the wall, option B is not correct. Also, this heat generation will make some portion of the wall at higher temp. than 100 deg. Celsius.
Correct Answer: D
Solved Example: 80-4-02
A freezer compartment consists of a cubical cavity that is 2 m on a side. Assume the bottom to be perfectly insulated. What is the minimum thickness of Styrofoam insulation (k=0.030 W/m.K) which must be applied to the top and side walls to ensure a heat load less than 500 W, when the inner and outer surfaces are -10 $^\circ$ C and 35$^\circ$C?
A. 27 mm
B. 36 mm
C. 13.5 mm
D. 54 mm
\begin{align*} q &=kA\dfrac {\Delta t}{\Delta x}\\ \Delta x &=\dfrac {5\times 0.03\times 45\times 4}{500}\\ \Delta x &=0.054\ m =54\ mm \end{align*}
Correct Answer: D
Solved Example: 80-4-03
If the inner and outer walls of a sphere having surface areas of A$_1$ and A$_2$ and inner and outer radii r$_1$ and r$_2$ are maintained at t$_1$ and t$_2$, then rate of heat flow will be:
A. $\dfrac{k}{\sqrt{A_1A_2}}\dfrac{t_1\ -\ t_2}{r_2\ -\ r_1}$
B. $k\sqrt{A_1A_2}\dfrac{t_1\ -\ t_2}{r_2\ -\ r_1}$
C. $4\pi k\dfrac{t_1\ -\ t_2}{\sqrt{A_1A_2}}$
D. $4\pi kr_1r_2\dfrac{t_1\ -\ t_2}{\sqrt{A_1A_2}}$
Correct Answer: B
Solved Example: 80-5-01
Hot air at a temp. of 60 $^{\circ}\mathrm{C}$ is flowing through a steel pipe of 100 mm diameter. The pipe is covered with two layers of different insulating layers of thickness 50 and 30 mm and their thermal conductivities are 0.23 and 0.37 W/m $^{\circ}\mathrm{C}$. The inside and outside heat transfer coefficients are 58 and 12 W/sq m$^{\circ}\mathrm{C}$.the atm temperature is at 25$^{\circ}\mathrm{C}$. Find the rate of heat loss from a 50 m length of pipe.
A. 1.971 kW
B. 2.334 kW
C. 3.018 kW
D. 1.441 kW
Inside heat transfer resistance \[\begin{split}
\dfrac{1}{h_i A} & = \dfrac{1}{58 \times 2\pi \times 50 \times
10^{-3} \times 50} = 1.097 \times 10^{-3} \dfrac{K}{W}
\end{split}\] Outside heat transfer resistance \[\begin{split}
\dfrac{1}{h_o A} & = \dfrac{1}{12 \times 2\pi \times 130 \times
10^{-3} \times 50} = 2.04 \times 10^{-3} \dfrac{K}{W}
\end{split}\] Inside insulation heat transfer resistance \[\begin{split}
\dfrac{ln \left(\dfrac{r_2}{r_1}\right)}{2 \pi K L} & = \dfrac{ln
\left(\dfrac{100}{50}\right)}{2 \pi \times 0.23 \times 50} = 9.59 \times
10^{-3} \dfrac{K}{W}
\end{split}\] Outside insulation heat transfer resistance \[\begin{split}
\dfrac{ln \left(\dfrac{r_3}{r_2}\right)}{2 \pi K L} & = \dfrac{ln
\left(\dfrac{130}{100}\right)}{2 \pi \times 0.37 \times 50} = 2.257
\times 10^{-3} \dfrac{K}{W}
\end{split}\] Total heat transfer resistance = 14.984 \(\times 10^{-3} \dfrac{K}{W}\)
Rate of Heat loss = \(\dfrac{T_2 -
T_1}{R_{Total}}\) = \(\dfrac{60-25}{14.984 \times 10^{-3} }\)=
2.334 kW
Correct Answer: B
Solved Example: 80-6-01
A composite wall is made of two layers of 0.3 m and 0.15 m thickness with surfaces held at 600$^{\circ}\mathrm{C}$ and 20$^{\circ}\mathrm{C}$ resp. If the conductivities are 20 and 50 W/mK, determine the heat conducted. In order to restrict the heat loss to 5 kW/m$^2$ another layer of 0.15 m thickness is proposed. Determine the thermal conductivity of the material required.
A. 15.22 KW, 2.85W/mK
B. 23.19 KW, 0.23W/mK
C. 32.22 KW, 1.53W/mK
D. 55.32 KW, 1.23W/mK
Part I: \begin{align*} R &= \dfrac{L_1}{K_1A} + \dfrac{L_2}{K_2A}\\ &= \dfrac{0.3}{20} + \dfrac{0.15}{50}\\ &= 0.018 \end{align*} \begin{align*} Q &= \dfrac{\Delta T}{R} \\ &= \dfrac{600 - 20}{0.018} \\ &= 32222\ W \end{align*} Part II: With the new insulation added: \begin{align*} Q &= \dfrac{\Delta T}{R} \\ 5000 &= \dfrac{600 - 20}{R}\\ R &= 0.116 \end{align*} This is in addition to the old resistance. \begin{align*} 0.018 + R_{insulation} &= 0.116\\ R_{insulation} &= 0.098\\ \dfrac{L_}{K_A} &= 0.098\\ k &= 1.531\ W/mK \end{align*}
Correct Answer: C
Solved Example: 80-6-02
A flat wall of a furnace is made up of fire brick, insulating brick and building brick of thicknesses 25 cm, 12.5 cm and 25 cm resp. The inside wall is at a temperature of 600 $^{\circ}\mathrm{C}$ and atm. Temperature is 20 $^{\circ}\mathrm{C}$. If the heat transfer coefficient for the outer surface is 10 W/sq m deg C, calculate the loss per sq meter of wall area. Take: K of wall brick=1.4 W/m $^{\circ}\mathrm{C}$, K of insulating brick= 0.2 W/m $^{\circ}\mathrm{C}$, K of fire brick= 0.85 W/m $^{\circ}\mathrm{C}$.
A. 0.48 kW per sq m
B. 1.16 kW per sq m
C. 0.86 kW per sq m
D. 2.94 kW per sq m
Total heat transfer resistance \begin{equation*} \begin{split} & = \dfrac{25 \times 10^{-2}}{0.85 \times 1} + \dfrac{12.5 \times 10^{-2}}{0.2 \times 1}\\ & + \dfrac{25 \times 10^{-2}}{1.4 \times 1} + \dfrac{1}{10 \times 1} = 1.198 \dfrac{K}{W} \end{split} \end{equation*} Rate of heat transfer = $\dfrac{600 - 20}{1.198}$ = 484 W per sq m = 0.48 kW per sq m
Correct Answer: A
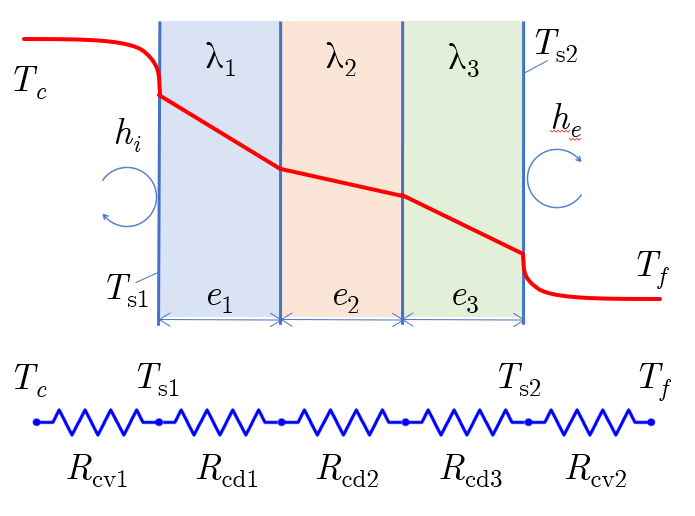
Composite Plane Wall
Learning Objectives:
- Draw the thermal circuit for multi layer composite wall.
Steps for calculating heat transfer rate for a composite wall having multiple layers of insulation. For more details, refer solved problem for the same chapter.
-
Calculate convection resistance for the inside air film using \(R_i = \dfrac{1}{h_iA}\)
-
Calculate convection resistance for the outside air film using \(R_o = \dfrac{1}{h_oA}\)
If these h values are not specified in the problem, then it is assumed that they do not contribute much towards the overall heat transfer resistance and hence the above two terms can be neglected. -
Calculate conduction resistance for first insulation using \(R = \dfrac{L}{kA}\) for plane wall or \(R = \dfrac{ln\left(\dfrac{r_2}{r_1}\right)}{2\pi k L}\) for cylindrical wall.
-
repeat this process for all insulation.
-
Add all these resistances in case of series combination. If any two or more resistances are parallel then use parallel resistance formula for that combination only.
-
Calculate the overall heat transfer.
-
if junction (boundary) temperatures are required, then consider resistances only upto that point.
Conduction Through a Plane Wall
Learning Objectives:
- To calculate conduction heat flow in a plane wall by thermal conduction in steady state conditions.
Solved Example: 9527-01
The dimensions of a wall are 5 m long, 10 m wide and 0.25 m thick, made of material having thermal conductivity at 1 W/mK. The temperature of inner and outside wall are 25 $^\circ$C and 15 $^\circ$C respectively for 10 hrs. If cost of electricity is \$0.15 per kWh, the cost of heat loss will be (in \$):
A. 0.3
B. 3
C. 25
D. 30
\begin{align*} Q &= \dfrac{T_2 - T_1}{\left(\dfrac{t}{kA}\right)}\\ &= \dfrac{25 - 15}{\left(\dfrac{0.25}{1 \times 5 \times 10}\right)}\\ &= 2000\ \mathrm{W}\\ &= 2\ \mathrm{kW} \end{align*} \[\mathrm{Cost\ of\ electricity}= 2 \times 10 \times 0.15 = \$3\]
Correct Answer: B
Conduction Through a Cylindrical Wall
Learning Objectives:
- Analytical solutions for heat conduction through orthogonal cylindrical and spherical walls.

DelPaine, CC BY-SA 4.0, via Wikimedia Commons
Solved Example: 9528-01
A stainless steel tube (k$_s$ = 19 W/m K) of 2 cm ID and 5 cm OD is insulated with 3 cm thick asbestos (k$_a$ = 0.2W/m K). If the temperature difference between the innermost and outermost surfaces is 600$^\circ$C, the heat transfer rate per unit length is:
A. 0.94 W/m
B. 9.44 W/m
C. 944.72 W/m
D. 9447.21 W/m
\begin{align*} \dfrac{Q}{l} &= \dfrac{T_1 - T_0}{ \dfrac{1}{2 \pi k_s} \ln \left(\dfrac{r_2}{r_1}\right) + \dfrac{1}{2 \pi k_a} \ln \left(\dfrac{r_3}{r_2}\right) }\\ &= \dfrac{600}{ \dfrac{1}{2 \pi \times 19} \ln \left(\dfrac{0.025}{0.01}\right) + \dfrac{1}{2 \pi \times 0.2} \ln \left(\dfrac{0.055}{0.025}\right) }\\ &= 944.72\ \mathrm{W/m} \end{align*}
Correct Answer: C
Solved Example: 9528-02
When two fluids of the heat exchanger are separated by a cylindrical wall, the thermal resistance comprises:
- Convection resistance due to the fluid film at the inside surface
- Conduction resistance
- Convection resistance due to the fluid film at the outside surface
A. 1 and 2
B. 1, 2 and 3
C. 2 and 3
D. 1 and 3
Correct Answer: B
Approximate Solution for Solid with Sudden Convection
Learning Objectives:
- Define Fourier Number as a dimensionless parameter.
- Explore the use of approximate solutions and correlations to estimate heat transfer coefficients and temperature profiles in situations involving convection.
For plane walls,
For infinite cylinders and spheres,
Solved Example: 9529-01
The dimensionless numbers used for analyzing the transient heat conduction problems in a plane wall, cylinder, and sphere are:
A. Nusselt Number and Fourier Number
B. Reynolds Number and Biot Number
C. Biot Number and Fourier Number
D. Nusselt Number and Biot Number
Correct Answer: C