Learning Objectives:

• Calculate the impedance, phase angle, power, power factor, voltage, and/or current in a RLC series circuit consisting of any combination of resistors, capacitors, and inductors.
• Express total impedance in rectangular and polar forms.
• Sketch an impedance triangle.

Solved Example: 20-1-02

When the frequency of the voltage applied to a series RC circuit is increased, the phase angle:

A. Decreases

B. Increases

C. Becomes erratic

D. Remains the same

In AC circuits, capacitive reactance is calculated using the following formula and plotted vertically downwards. \[X_C = \dfrac{1}{2 \pi f C}\] Since the capacitive reactance is inversely proportional to the frequency, as frequency increases, capacitive reactance decreases. Power triangle becomes smaller as the vertical side of the power triangle decreases. Hence, phase angle decreases.

Correct Answer: A

Solved Example: 20-1-04

To increase the current in a series RL circuit, the frequency:

A. Should be constant

B. Cannot be determined without values

C. Should be increased

D. Should be decreased

The value of resistance is independent of frequency. However, Inductance $ X_{L} = 2 \pi f L$ is directly proportional to the frequency, due to which Impedance increases with increase in frequency.
As frequency increases, Impedance increases, and current decreases. To avoid this, frequency must be decreased to get higher values of current.

Correct Answer: D

Solved Example: 20-1-05

A 12 k$\Omega$ resistor is in series with a 90 mH coil across an 8 kHz AC source. Current in the circuit, expressed in polar form, is I = 0.30 $\angle$ 0 mA. The source voltage, expressed in polar form, is:

A. 3.84 $\angle$ 20.6 V

B. 0.32 $\angle$ 0.6 V

C. 12.8 $\angle$ 20.6 V

D. 13.84 $\angle$ 69.4 V

$f=8kHz$, $i=0.30\times 10^{-3} \angle 0,$
\[X_{L} =2\pi fL=2\pi \left( 8000\right) \left( 90\times 10^{-3}\right) = 4.524\ k\Omega\] \[Z =\sqrt {R^{2}+X_{L}^{2}}=\sqrt {12^{2}+4.524^{2}}=12.824\ k\Omega\] \[\phi =\tan ^{-1}\left( \dfrac {X_{L}}{R}\right) =\tan^{-1}\left( \dfrac {4.524}{12}\right) =20.6^\circ\] \begin{align*} Z &=\dfrac {V}{i} \\ 12.824 \angle 20.6^\circ &=\dfrac {V}{0.30\times 10^{-3} \angle 0} \\ V &=3.85 \angle 20.6^\circ \end{align*}

Correct Answer: A

Solved Example: 20-1-06

A 1.5 k$\Omega$ resistor and a coil with a 2.2 k$\Omega$ inductive reactance are in series across an 18 V AC source. The power factor is:

A. 0.922

B. 0.564

C. 0.76

D. 0.557

$\tan \phi = \dfrac{2.2}{1.5}, \quad \phi = \tan^{-1} \left(\frac{2.2}{1.5} \right) = 55.7^\circ$ \[\mathrm{Power\ Factor} = \cos \phi = \cos (55.7^\circ) = 0.564\]

Correct Answer: B

Solved Example: 20-1-07

In a series circuit, R = 300 $\Omega$, L = 0.9 H, C = 2.0 $\mu$ F and $\omega$ = 1000 rad/sec. The impedance of the circuit is:

A. 900 $\Omega$

B. 500 $\Omega$

C. 400 $\Omega$

D. 1300 $\Omega$

\[X_L = \omega L = (1000)\times (0.9)=900\ \Omega\] \[X_C = \dfrac{1}{\omega C} = \dfrac{1}{1000 \times 2\times 10^{-6}}= 500\ \Omega\] \[Z = \sqrt{R^2 + (X_L - X_C)^2} \\ = \sqrt{300^2 + 400^2} = 500\ \Omega\]

Correct Answer: B

Solved Example: 20-1-08

When 100 volts DC is supplied across a solenoid (Resistance and inductor in series), a current of 1.0 A flows in it. When 100 volts AC is applied across the same coil, the current drops to 0.5 A. If the frequency of AC source is 50 Hz, then the impedance and inductance of the solenoid are:

A. 200$\Omega$, 0.55H

B. 100$\Omega$, 0.86H

C. 200$\Omega$, 1.0H

D. 100$\Omega$, 0.93H

For DC, Inductor part will not be effective. \[ R = \dfrac{V}{i} = 100\ \Omega\] For AC, \[ Z = \dfrac{V}{i} = \dfrac{100}{0.5} = 200\ \Omega\] \begin{align*} Z &= \sqrt{R^2 + (X_L)^2}\\ 200^2 &= 100^2 + (X_L)^2\\ X_L &= 173.2\ \Omega \end{align*} Given f = 50 Hz and Using, \[X_L = 2 \pi f L\] \[L = 0.55\ H\]

Correct Answer: A

Solved Example: 20-1-09

The potential difference V and the current i flowing through an instrument in an AC circuit of frequency f are given by V=5 $\cos \omega$t volts and I = 2 $\sin \omega$t amperes (where $\omega$ = 2$\pi$f). The power dissipated in the instrument is:

A. Zero

B. 10 W

C. 5 W

D. 2.5 W

\[V=5 \cos \omega t=5 \sin( \omega t + \dfrac{\pi}{2})\] and \[i=2 \sin \omega t\] \[\mathrm{Power} = V_{RMS} \times i_{RMS} \times \cos \phi = 0\] (Since $\phi = \dfrac{\pi}{2}$, therefore $\cos \phi =\cos \dfrac{\pi}{2}$=0)

Correct Answer: A

Solved Example: 20-1-10

A resistance R and a capacitor C connected in series across a 250V supply draw 5A at 50Hz. When frequency is increased to 60Hz, it draws 5.8A. Find the value of C.

A. 69.4 $\mu$F

B. 122.4 $\mu$F

C. 220.7 $\mu$F

D. 371.9 $\mu$F

Case I: When f = 50 Hz
\[Z=\dfrac{V}{I} = \dfrac {250}{5}=50\ \Omega\] \[X_{C}=\dfrac {1}{2\pi fC}=\dfrac {1}{2\pi \left( 50\right) C}=\left( \dfrac {3.18\times 10^{-3}}{C}\right) \Omega\] \begin{align*} Z^{2}&=R^{2}+{X_C}^{2}\\ 2500&=R^{2}+\left( \dfrac {3.18\times 10^{-3}}{C}\right)^{2} \end{align*} Case II: When f = 60 Hz \[X_{C}=\dfrac {1}{120\pi C}= \dfrac{2.65\times 10^{-3}}{C}\ \Omega\] \[Z=\dfrac {250}{5.8}=43.10\ \Omega\] \[1857.9=R^{2}+\left( \dfrac {2.65\times 10^{-3}}{C}\right) ^{2}\] Subtracting I-II \begin{align*} 642.09 &=\dfrac {3.09\times 10^{-6}}{C^{2}}\\ C^{2} &=4.812\times 10^{-9}\\ C &=6.94\times 10^{-5}\ F =69.4\ \mu F \end{align*}

Correct Answer: A

Solved Example: 20-1-11

If the load impedance is 20 - j20, the power factor is:

A. $45^\circ$

B. 0

C. 1

D. 0.707

Impedance $Z = \sqrt{R^2 + X^2}$ \[Z = \sqrt{20^2 + (-20)^2} = 20\sqrt{2} \Omega\] Power factor is: \[\cos \phi = \dfrac{R}{Z} = \dfrac{20}{20\sqrt{2}} = 0.707\]

Correct Answer: D

Solved Example: 20-1-12

The phase voltage and current across a load element are 100.0 $\angle$ 45$^\circ$ V and 5.0 $\angle$15$^\circ$ A. respectively. Determine the impedance and admittance of the load.

A. Z = 20.0 $\angle$-30$^\circ$ Ω and Y = 0.05$\angle$30$^\circ$ S

B. Z = 20.0 $\angle$30$^\circ$ Ω and Y = 0.05$\angle$-30$^\circ$ S

C. Z = 0.05 $\angle$30$^\circ$ Ω and Y = 20$\angle$-30$^\circ$ S

D. Z = 0.05$\angle$-30$^\circ$ Ω and Y = 20 $\angle$30$^\circ$ S

\[Z = \dfrac{V}{I} = \dfrac{100 \angle 45}{5 \angle 15} = 20 \angle 30^\circ\] \[Y =\dfrac{1}{Z} = \dfrac{1}{20\angle 30} 0.05\angle -30^\circ\]

Correct Answer: B

Solved Example: 23423

The unit of impedance is:

A. Ohm

B. Farad

C. Henry

D. Volt

Correct Answer: A

Solved Example: 234234

In a series RLC circuit, how does the total impedance change when the frequency increases?

A. Increases

B. Decreases

C. Remains constant

D. Cannot be determined

Correct Answer: B

Solved Example: 234234

Which of the following statements about impedance is true?

A. Impedance only applies to resistors.

B. Impedance can only be calculated at DC.

C. Impedance combines resistance and reactance.

D. Impedance does not affect power in a circuit.

Correct Answer: C

Solved Example: 234234

When analyzing a series RLC circuit at resonance, what is the relationship between current and voltage?

A. They are out of phase.

B. They are in phase.

C. Current leads voltage.

D. Voltage leads current.

Correct Answer: B

Solved Example: 345345

Which component contributes a negative reactance in an AC circuit?

A. Resistor

B. Inductor

C. Capacitor

D. None of the above

Correct Answer: C

Solved Example: 43345

What does the term "reactance" refer to in AC circuits?

A. Resistance to DC

B. Resistance to AC caused by capacitance or inductance

C. Total opposition to current

D. None of the above

Correct Answer: B

Learning Objectives:

• Calculate average value of a waveform and state its significance.
• Calculate average value of some standard types of waveforms.

Average Value: The arithmetic average of all the values of an alternating quantity over one cycle is called its average value.

For Symmetrical waveforms, the average value calculated over one cycle becomes equal to zero because the positive area cancels the negative area. Hence for symmetrical waveforms, the average value is calculated for half cycle.

Solved Example: 20-2-01

For the same peak value, which of the following wave has the least mean value ?

A. Half wave rectified sine wave

B. Triangular wave

C. Sine wave

D. Square wave

Half wave rectified sine wave has zero value for half cycle corresponding to the negative half cycle of input waveform. Hence, it's mean value is lesser that the remaining, for same peak value.

Correct Answer: A

Solved Example: 20-2-02

The average value of the periodic waveform shown in the following figure is:

A. 1.414 V

B. 2 V

C. 2.4 V

D. 2.5 V

The average voltage (or current) of a periodic waveform is defined as the area under the waveform divided by time.
In other words, the averaging of all the instantaneous values along time axis with time being one full period, (T).

Correct Answer: B

Learning Objectives:

• Calculate the root-mean-square (RMS) value of a waveform.
• Calculate the RMS values of some standard waveforms.

The effective or RMS value of an alternating quantity is that steady current (DC) which when flowing through a given resistance for a given time produces the same amount of heat produced by the alternating current flowing through the same resistance for the same time.

$X_{\mathrm{eff}} =X_{\mathrm{RMS}}=\left [ \dfrac{1}{T} \displaystyle \int_{0}^{T}x^{2}(t)dt \right ]^{\frac{1}{2}}$       Page 362

AlanM1, CC0, via Wikimedia Commons

RMS Values of Some Standard Waveforms:

RMS value of a sinusoidal waveform and full wave rectified sine wave:

$X_{RMS}= \dfrac{X_{max}}{\sqrt{2}} = 0.707 X_{max}$       Page 362

RMS value of a half wave rectified sine wave:

$X_{RMS}= \dfrac{X_{max}}{2} = 0.5 X_{max}$       Page 362

If a waveform is periodic:

$X_{RMS} = \sqrt{X_{DC}^2 + \sum_{n=1}^{\infty} X_n^2}$       Page 362

where,
X$_{DC}$ = DC component of waveform (vertical shift of mean value of wavefrom from x-axis
X$_n$= RMS value of the n$^{th}$ harmonic

Omegatron, CC BY-SA 3.0, via Wikimedia Commons

Full Wave-Wave rectified Sine Wave
Zureks, CC BY-SA 3.0, via Wikimedia Commons

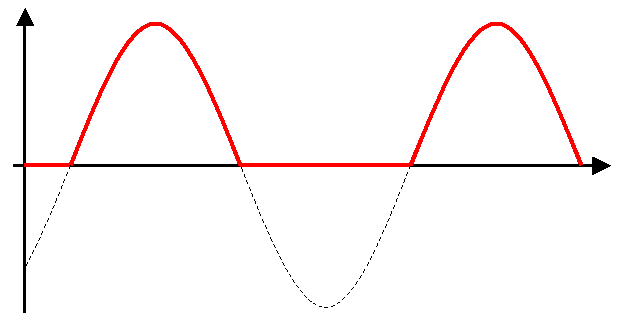
Half-Wave rectified Sine Wave
Zureks, CC BY-SA 3.0, via Wikimedia Commons

Solved Example: 20-3-01

The R.M.S. value and mean value is the same in the case of:

A. Triangular wave

B. Sine wave

C. Square wave

D. Half wave rectified sine wave

In case of DC, mean (average), RMS and instantaneous values are same.
In case of symmetrical square wave (square wave with equal positive and negative peaks) also, RMS value = mean value = peak value.

Correct Answer: C

Solved Example: 20-3-02

For the same peak value which of the following wave will have the highest R.M.S. value?

A. Square wave

B. Half wave rectified sine wave

C. Triangular wave

D. Sine wave

To get a high RMS value, you want a waveform that is as high as possible most of the time, which happens in case of square wave as the instantaneous value is constant (and high) for half cycle. Since the values are squared while calculating RMS values, during negative half also, same effect takes place.

Correct Answer: A

Solved Example: 20-3-03

For a sine wave with peak value I$_{max}$ the R.M.S. value is:

A. 0.5 I$_{max}$

B. 0.707 I$_{max}$

C. 0.9 I$_{max}$

D. 1.414 I$_{max}$

\begin{align*} i_{RMS} &= \left[\dfrac{1}{\pi}\int_{0}^{\pi}i^{2}(t)dt \right ]^{\frac{1}{2}}\\ &=\left[\dfrac{I_{max}^2}{\pi}\int_{0}^{\pi} \sin ^2 t\ dt \right ]^{\frac{1}{2}}\\ &= \dfrac{I_{max}}{\sqrt{2}\sqrt{\pi}}\left[\int_{0}^{\pi} (1- \cos 2t)\ dt \right ]^{\frac{1}{2}}\\ &= \dfrac{I_{max}}{\sqrt{2}\sqrt{\pi}}\left[ \left(t- \dfrac{\sin 2t}{2}\right)_0^\pi \right ]^{\frac{1}{2}}\\ &= \dfrac{I_{max}}{\sqrt{2}\sqrt{\pi}}\left[ (\pi - 0)-(0-0)\right]^{\frac{1}{2}}\\ &= \dfrac{I_{max}\sqrt{\pi}}{\sqrt{2}\sqrt{\pi}} = \dfrac{I_{max}}{\sqrt{2}} = 0.707I_{max} \end{align*}

Correct Answer: B

Solved Example: 20-3-04

A light bulb is rated at 100W for a 220 V supply. The peak voltage of the source is:

A. 220 V

B. 155.56 V

C. 311 V

D. Cannot be determined

The peak voltage of the source for bulb rated V volts is $\sqrt{2}$ V Hence,
Peak voltage= $\sqrt{2}$ $\times$ 220V =311V

Correct Answer: C

Solved Example: 20-3-05

The RMS value of the periodic waveform shown in the following figure is:

A. 0.96 V

B. 2.35 V

C. 2.5 V

D. 4.9 V

The RMS voltage (or current) of a periodic waveform is defined as the effective value equivalent of a steady DC (constant) value which gives the same effect. \begin{align*} V_{RMS} &= \left[\dfrac{1}{T}\int_{0}^{T}v^{2}(t)dt \right ]^{\frac{1}{2}}\\ &=\left[\frac{1}{6}\int_{0}^{2}v^{2}(t)dt + \int_{2}^{5}v^{2}(t)dt + \int_{5}^{6}v^{2}(t)dt\right]^{\frac{1}{2}}\\ &=\left[\dfrac{1}{6}\int_{0}^{2}(1.5t)^{2}dt + \int_{2}^{5}(3)^{2}dt + \int_{5}^{6}0^{2}dt\right]^{\frac{1}{2}}\\ &= \left[\dfrac{1}{6}\left(6 + 27 + 0\right) \right]^{\frac{1}{2}}\\ &= 2.35\ V \end{align*}

Correct Answer: B

Learning Objectives:

• Identify the components of complex power.
• Compute complex power given AC voltage and current either in terms of peak values or RMS values.
• Draw power triangle.

Real Power:

\begin{align*} P &= V_{RMS} I _{RMS} \cos \theta\\ &= \left(\dfrac{V_{max}}{\sqrt{2}}\right) \left(\dfrac{I_{max}}{\sqrt{2}}\right) \cos \theta\\ &= \dfrac{1}{2}V_{max} I _{max} \cos \theta \end{align*}

Reactive Power:

\begin{align*} Q &= V_{RMS} I _{RMS} \sin \theta\\ &= \left(\dfrac{V_{max}}{\sqrt{2}}\right) \left(\dfrac{I_{max}}{\sqrt{2}}\right) \sin \theta\\ &= \dfrac{1}{2}V_{max} I _{max} \sin \theta \end{align*}

Complex Power:

\[S = VI^* = P + jQ\] where I$^*$ = complex conjugate of the phasor current.

Wikieditor4321, CC BY-SA 4.0, via Wikimedia Commons

Solved Example: 20-4-01

The voltage across the circuit in the figure, and the current through it, are given by the following expressions:

where $\omega$ = 100$\pi$ radian/s. If the average power delivered to the circuit is zero, then the value of X (in Ampere) is:

A. 10

B. 20

C. 30

D. 40

Correct Answer: A

Solved Example: 20-4-02

Average power delivered to impedance $(4 - j3) \Omega$ by a current $5 \cos (100 \pi t + 100) A$:

A. 44.2 W

B. 50 W

C. 62.5 W

D. 125 W

\[Z = \sqrt{4^2 + 3^2} = 5\ \Omega\] \[\cos \phi = \dfrac{4}{5} = 0.8\] \[I_{RMS} = 0.707 I_{max} = 0.707 \times 5 = 3.535\ A\] \[P = I^2 Z \cos \phi = (3.535)^2 \times 5 \times 0.8 = 50\ W\]

Correct Answer: B

Solved Example: 20-4-03

A source $V_s = 200 \cos \omega t$ delivers power to a load at power factor 0.8 lag. The reactive power is 300 VAR. The active power is given by?

A. 200 Watts

B. 225 Watts

C. 400 Watts

D. 300 Watts

\[\sin \phi = \sqrt{1 - \cos^2\phi} = 0.6\] \[Q= 300\ VAR\] \[Q = VI \sin \phi\] \[300 = VI \sin \phi\] \[VI = 500\ VA\] \[P = VI \cos \phi = 500 (0.8) = 400\ W\]

Correct Answer: C

Solved Example: 20-4-04

The unit for Reactive power is:

A. kVAR

B. kVA

C. kW

D. None of the above

Correct Answer: A

Solved Example: 20-4-05

Three loads are connected in parallel cross a 1-phase, 1200 V, 50 Hz supply.

Load 1: Capacitive load, 10 kW and 40 kVAR

Load 2: Inductive load, 35 kW and 120 kVAR

Load 3: Resistive load of 15 kW

A. (10 + j80) kVA

B. (60 + j160) kVA

C. (10 - j160) kVA

D. (60 + j80) kVA

In parallel circuits, branch powers are added. \[P = P_1 + P_2 + P_3\] For load#1 : \[P_1 = (10 - j40)\ kVA\] For load#2 : \[P_2 = (35 + j120)\ kVA\] For load#3 : \[P_3 = 15\ kW\] \begin{align*} P &= P_1 + P_2 + P_3\\ &= 10 - j40 + 35 + j120 + 15\\ &= 60 + j80 \end{align*}

Correct Answer: D

Solved Example: 20-4-06

Find the power p(t), supplied by the element when $v(t) = 4 \cos 3t V$ and $i\left( t \right) = \dfrac{1}{{12}}\sin 3t\ A$

A. $p\left( t \right) = \dfrac{1}{6}\cos 6t\ W$

B. $p\left( t \right) = \dfrac{1}{6}\sin 3t\ W$

C. $p\left( t \right) = \dfrac{1}{{12}}\sin 6t\ W$

D. $p\left( t \right) = \dfrac{1}{6}\sin 6t\ W$

Instantaneous power supplied, \begin{align*} P(t) &= V(t) \cdot I(t)\\ &= 4 \cos 3t \times \dfrac{1}{{12}}\sin 3t\\ &= 4 \left(\dfrac{1}{{12}}\right) \times \cos 3t \times \sin 3t\\ &= 2 \left(\dfrac{1}{{12}}\right) \times (2\cos 3t \times \sin 3t)\\ &= \dfrac{1}{{6}} \times (\sin 6t) \end{align*}

Correct Answer: D